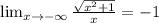Найти предел функции при sgrt(x*2 + 1)/x при х стремящемуся к минус бесконечности
Другие вопросы по теме Математика
Популярные вопросы
- Схарактерезуйте безособові дієслівні форми на - но ,- то , навидіть приклади...
3 - Как решить ? на лодочной станции 150 лодок, из которых трёхместных-14%. число...
3 - Как пишется салат оливье или оливье...
2 - Все , с 1)определи правильность утверждений. 1. при комнатной температуре активность...
3 - Пересказ капитанская дочка с 1 по 5 главу, кратко,...
3 - Особенности поэзий магжана жумабаева, 24...
3 - Нипишите краткий анализ стихотворения тютчева весенние воды оч спешу...
2 - Соотнесите слова из левого столбика с их синонимами из правого: а) неправильный;...
1 - Найти производную: y=4sin(x)/cos^2(x) ,...
2 - Вклассе 25 учеников, из них 10 человек получили отлично по в четверти. для участия...
3
Сначала учтем, что поскольку у нас стремление к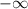 то х будет отрицательным. Дальше преобразуем выражение:
то х будет отрицательным. Дальше преобразуем выражение:
Теперь находим предел:
Почему -1, потому что по сути в числителе у нас явно положительное число, и после наших преобразований оно и должно им остаться. а вот знаменатель при стремлении к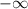 будет отрицательным. Если делить положительное на отрицательное, то в результате получается отрицательное.
будет отрицательным. Если делить положительное на отрицательное, то в результате получается отрицательное.
ответ: