1. Математика
  2. Найти предел функции,

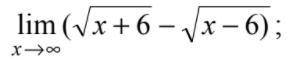
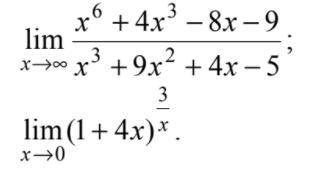
Найти предел функции, используя правило Лопиталя


Найти предел функции, используя правило Лопиталя
Найти предел функции, используя правило Лопиталя

slava285 slava285    3   04.12.2021 22:42    0

Ответы
Димончик111111 Димончик111111  19.01.2022 21:56

1. Конечно, этот предел проще вычислить без правила Лопиталя, но если  нужно ...

\lim\limits_{x\to +\infty}\left(\sqrt{x+6}-\sqrt{x-6}\right)=\lim\limits_{x\to +\infty}\sqrt{x}\left(\sqrt{1+\frac{6}{x}}-\sqrt{1-\frac{6}{x}}\right)=\left|\left|\dfrac{1}{\sqrt{x}}=t\right|\right|=

=\lim\limits_{t\to 0}\dfrac{\sqrt{1+6t^2}-\sqrt{1-6t^2}}{t}=\left[\dfrac{0}{0}\right]=\lim\limits_{t\to 0}\dfrac{\left(\sqrt{1+6t^2}-\sqrt{1-6t^2}\right)'}{t'}=

\lim\limits_{t\to 0}\left(\dfrac{12t}{2\sqrt{1+6t^2}}+\dfrac{12t}{2\sqrt{1-6t^2}}\right)=0.

2.  И в этой задаче Лопиталь ни при чем...

\lim\limits_{x\to \infty}\dfrac{x^6+4x^3-8x-9}{x^3+9x^2+4x-5}=\left[\dfrac{\infty}{\infty}\right]=\lim\limits_{x\to \infty}\dfrac{6x^5+12x^2-8}{3x^2+18x+4}=\left[\dfrac{\infty}{\infty}\right]=

=\lim\limits_{x\to\infty}\dfrac{30x^4+24x}{6x+18}=\left[\dfrac{\infty}{\infty}\right] = \lim\limits_{x\to\infty}\dfrac{120x+24}{6}=\infty.

3. ответ, как и в двух предыдущих задачах, можно написать сразу...

\lim\limits_{x\to 0}(1+4x)^{3/x}=\lim\limits_{x\to 0} e^{\ln(1+4x)^{3/x}}=e^{\lim\limits_{x\to 0}\frac{3}{x}\ln(1+4x)}=e^{3\lim\limits_{x\to 0}\frac{ln(1+4x)}{x}}=\left[\dfrac{0}{0}\right]=

=e^{3\lim\limits_{x\to 0}\frac{4}{1+4x}}=e^{12}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
КариM КариM  07.09.2019 17:00
Изобразите систему координат oxyz и постройте точку а(-1; 2; 4). найдите расстояние от этой точки до координатных плоскостей....
Русель Русель  07.09.2019 17:00
Тема пропорциональность. для приготовления начинки для пирога взяли курагу с черносливом в отношении 4: 1. найдите массу каждого компонента в 35 кг начинки?...
kogoch kogoch  07.09.2019 17:00
Разложите на множители: (х+2у)*(х+2у+-1)*(у+1)...
ya042302SashaA ya042302SashaA  07.09.2019 17:00
Запишите выражение без скобок и найдите его значение а) (-35)+(-5)= б) (++8)= в) (-)= г) (+16)+(-48)= д) (-+11)= е) (+)=...
jojo31 jojo31  07.09.2019 17:00
Каждую букву замени цифрой так, чтобы получилось верное арифметическое равенство. одинаковым буквам соответствуют одинаковые цифры, разным буквам – разные цифры. известно, что буква...
миккимаус1890677 миккимаус1890677  07.09.2019 17:00
Унаргиз было 53 mammoth после того как она купила настольную лампу у неё осталось 39 манат сколько стоит настольная лампа?...
хааа2 хааа2  07.09.2019 17:00
Токарь может обточить 4316 заготовки за 13 дней, а его ученику на выполнение той же работы требуется в 4 раза больше времени. токарь и ученик обточат 2905 такие заготовки при совместной...
ponia ponia  07.09.2019 17:00
Поставь между цифрами 1,2.3.4.5.6.7.8.9 знаки сложения и вычитания чтобы значение полученного выражения равнялось 100...
dianka0202 dianka0202  07.09.2019 17:00
Вкуске сплава содержится никеля на 40 г.больше чем меди,а меди в 5 раз меньше чем никеля.сколько граммов каждого метала содержится в куске сплава...
домкорытосыгуьдатсс домкорытосыгуьдатсс  07.09.2019 17:00
Решите уравнение: х : 1 5/31 = 7 3/4 : 1/3...

Популярные вопросы