Найти поток векторного поля F через поверхность S в направлении внешней нормали. F=
S- верхняя полусфера:
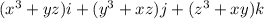
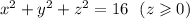
Другие вопросы по теме Математика
Популярные вопросы
- На підводу поклали 4 мішки жита і 3 мішки пшениці. скільки кілограмів...
3 - Маятник совершил 40колебаний за 160с. найти период и частоту колебаний...
2 - Дима,ваня и сережа съели семь конфет.все они съели разное количество конфет.дима...
1 - Перевести текст в.г. белинский сравнивает искусство с живым человеческим...
3 - Напишите уравнение реакции воды и уксуса...
1 - Велечины х и y наход в прямо пропрц зависимости и к = 2 1)запишите ыормулу...
2 - Как записать предложения: : вчера рози готовила. вчера алиса мыла посуду....
3 - Вмагазин 164л подсолнечного масла и 3 одинаковых ёмкости с оливковым маслом....
3 - Укажите промежуток ,содержащий корень уравнения 2^x=8...
3 - Периметр прямоугольника равен 16см.какими могут быть длины его сторон,выраженные...
3
Формула потока через поверхность:
Φ = ∬ F · dS
где F - векторное поле, dS - элемент площади поверхности, а ∬ представляет собой двойной интеграл по поверхности S.
Для начала, мы должны выразить векторное поле F в виде координатных функций. Из данного уравнения:
F = (x^3 + yz)i + (y^3 + xz)j + (z^3 + xy)k
следует, что F(x, y, z) = (x^3 + yz)i + (y^3 + xz)j + (z^3 + xy)k.
Теперь давайте рассмотрим поверхность S, которая является верхней полусферой с радиусом 4 (из уравнения x^2 + y^2 + z^2 = 16) и z >= 0.
Чтобы использовать формулу потока через поверхность, нам необходимо задать параметризацию этой поверхности.
Поскольку наша поверхность является полусферой, выгодно использовать сферические координаты. Заменяя x, y и z следующим образом:
x = r*sin(phi)*cos(theta)
y = r*sin(phi)*sin(theta)
z = r*cos(phi)
Мы можем переписать уравнение поверхности S в сферических координатах:
r^2 = 16
z >= 0
Итак, поверхность S в сферических координатах:
S: 0 <= theta <= 2*pi
0 <= phi <= pi/2
0 <= r <= 4
Теперь мы готовы выразить поверхностный элемент dS в сферических координатах.
dS = |(∂r/∂theta) x (∂r/∂phi)| dθ dφ
∂r/∂theta = r*sin(phi)*(-sin(theta))
∂r/∂phi = r*cos(phi)
Таким образом,
dS = |(r*sin(phi)*(-sin(theta)))i + (r*cos(phi))j + (r*sin(phi)*cos(theta))k| dθ dφ
= r^2*sin(phi) dθ dφ
Заменяем значения переменных и выражаем векторное поле F в сферических координатах:
F = (r^3*sin(phi)*cos(theta) + r*sin(phi)*cos(theta)*r*cos(phi))i + (r^3*sin(phi)*sin(theta) + r*sin(phi)*sin(theta)*r*cos(phi))j + (r^3*cos(phi) + r*sin(phi)*r*sin(phi)*cos(theta))k
= (r^3*sin(phi)*cos(theta) + r^2*sin(phi)*cos(theta)*cos(phi))i + (r^3*sin(phi)*sin(theta) + r^2*sin(phi)*sin(theta)*cos(phi))j + (r^3*cos(phi) + r^2*sin^2(phi)*cos(theta))k
Теперь мы готовы вычислить поток векторного поля F через поверхность S в направлении внешней нормали.
Φ = ∬ F · dS
= ∬ [(r^3*sin(phi)*cos(theta) + r^2*sin(phi)*cos(theta)*cos(phi))i + (r^3*sin(phi)*sin(theta) + r^2*sin(phi)*sin(theta)*cos(phi))j + (r^3*cos(phi) + r^2*sin^2(phi)*cos(theta))k] · (r^2*sin(phi) dθ dφ)
= ∬ [r^5*sin^2(phi)*cos(theta) + r^4*sin^2(phi)*cos(theta)*cos(phi) + r^3*cos(phi)*sin(phi)] dθ dφ
Используя границы параметров поверхности S, диапазон значений theta и phi будет:
0 <= theta <= 2*pi
0 <= phi <= pi/2
Теперь мы можем выполнить интегрирование:
Φ = ∫[0 to pi/2] ∫[0 to 2*pi] [r^5*sin^2(phi)*cos(theta) + r^4*sin^2(phi)*cos(theta)*cos(phi) + r^3*cos(phi)*sin(phi)] dθ dφ
Вычисление этого интеграла может быть довольно сложным, и требует использования методов численного интегрирования или математического программного обеспечения.
Надеюсь, это помогло понять, как найти поток векторного поля F через поверхность S в направлении внешней нормали. Если у вас возникнут дополнительные вопросы, пожалуйста, дайте мне знать.