Найти площадь треугольника ABC. Напишите с подробным решением.
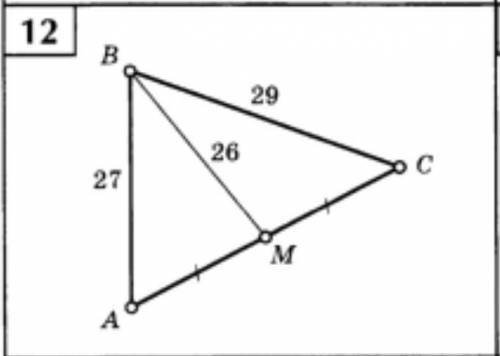
Другие вопросы по теме Математика
Популярные вопросы
- Обрати одну з поезій дракона і зробити ідейно-художній аналіз за зразком...
3 - сделайте все Выпишите из предложений все наречия. Запишите слова, от...
3 - В електричний чайник, опір спіралі якого становить 128Ом, налили 1кг...
3 - Write a blog about the UK (about 4 countries)...
3 - Найдите координаты точки пересечения прямых 4x=8 и x+11y=13 с объяснением...
1 - Розглянь наведену схему. Визнач послідовність етапів та підпиши кожен...
3 - який найбільший тиск на рейки створить двовісний залізничний вагон (4...
1 - Вычисли + 0,35 \(\) 0,05 \(\)=:=...
2 - У клітинах грибів відсутні: Вакуолі Пластиди • Мітохондрії Комплекс гольджі...
3 - Сравните древне Хорезмское и Кушанское царства....
2
Площадь треугольника = (Основание * Высота) / 2.
Однако, у нас есть некоторая проблема — нам не даны длины сторон треугольника и его высота, поэтому нам нужно найти их сначала.
Для начала, давайте обратим внимание на то, что треугольник ABC — прямоугольный треугольник. Мы это можем сказать, потому что угол ACB обозначен прямым значком (90°).
Итак, нам дано, что ACB = 90°. Это значит, что мы можем использовать теорему Пифагора, чтобы найти длину стороны BC (гипотенуза). Теорема Пифагора гласит:
c^2 = a^2 + b^2,
где c — гипотенуза, a и b — катеты. В нашем случае, сторона AC будет являться гипотенузой, а стороны AB и BC — катетами.
Давайте обозначим длину сторон AB, BC, и AC как a, b, и c соответственно.
С учетом этого, мы можем записать:
AC^2 = AB^2 + BC^2.
Теперь, используя значения, которые нам даны на рисунке, мы можем найти длину стороны BC:
AC^2 = 5^2 + 12^2.
AC^2 = 25 + 144.
AC^2 = 169.
AC = √169.
AC = 13.
Таким образом, длина стороны AC равна 13 единицам.
Теперь, чтобы найти площадь треугольника ABC, нам нужно найти его высоту. Мы можем использовать формулу для площади треугольника в терминах его сторон и высоты, которая гласит:
Площадь треугольника = (1/2) * основание * высота.
Мы знаем, что основание AB равно 5 единицам, а высоты к нему мы не знаем. Однако, мы можем заметить, что треугольник ABC разделен на два прямоугольных треугольника, поэтому его высота будет равна высоте одного из этих треугольников.
Давайте обозначим высоту треугольника ABC как h, и высоту разделенного прямоугольного треугольника как h1.
Теперь мы можем использовать подобие треугольников, чтобы найти отношение между высотами h и h1. Мы знаем, что треугольники ABC и CEB подобны, поэтому их стороны пропорциональны.
AB/AC = CB/CE.
Подставим значения:
5/13 = 12/h1.
Теперь найдем h1, перемножив и разделив значения:
5 * h1 = 13 * 12.
h1 = (13 * 12) / 5.
h1 = 156 / 5.
h1 = 31.2.
Таким образом, высота прямоугольного треугольника CEB равна 31.2 единицам.
Теперь, чтобы найти площадь треугольника ABC, мы можем использовать формулу:
Площадь треугольника = (Основание * Высота) / 2.
Площадь треугольника = (5 * 31.2) / 2.
Площадь треугольника = 156 / 2.
Площадь треугольника = 78.
Таким образом, площадь треугольника ABC равна 78 квадратным единицам.