Найти площадь фигуры, ограниченной линиями y=-x^2+2, y=x.
Другие вопросы по теме Математика
Популярные вопросы
- Запишите уравнения химических реакций (дальше на фото)...
3 - Напишите письменную работу выбрав в качестве темы один из афоризмов писателей...
3 - Как Алёхин познакомился с Лугановичем? Луганович был дальним родственником...
3 - Используя материалы учебника, книги «Читаем, думаем, спорим... 9 класс»...
2 - Вместо точек вставь в текст перечисленные термины: ДНК, иРНК, тРНК, аминокислоты,...
3 - Элементы технических систем II. Распределите элементы различных технических...
3 - 1. Выберите функции, графики которых параллельны, ответ обоснуйте: A) у=5х...
2 - Як називається півострів де жили вікінги ?...
2 - Вопрос 7 Соотнесите. Варианты ответов Швейная промышленность Текстильная...
2 - 856. Числа, которые делятся на 10, делятся ли: на 2; на 5?...
3
Найдём абсциссы точек пересечения графиков функций. Для этого необходимо приравнять данные функции и решить уравнение:
Теперь воспользуемся формулой Ньютона-Лейбница:
Где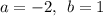 . Нам ничего не остаётся сделать, как подставить численные значения в формулу и решить определённый интеграл:
. Нам ничего не остаётся сделать, как подставить численные значения в формулу и решить определённый интеграл:
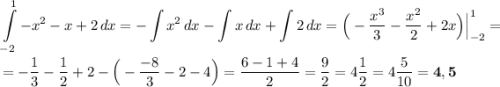
ответ: