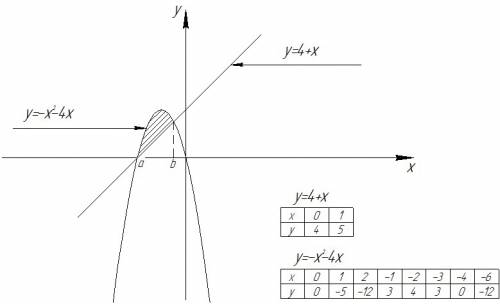
Найти площадь фигуры ограниченной графиками функции y=-x^2-4x и y=4+x
Ответы

 - пределы интегрирования. (на рисунке изображены как "a" и "b").
- пределы интегрирования. (на рисунке изображены как "a" и "b").
Другие вопросы по теме Математика
Популярные вопросы
- Сформулируйте предложения по афоризму имей смелость знать...
3 - Найти начальные формы слов сколько их? зелёный,зелёные зелёное,зелёных,зеленеет,зелёненький,зелёненькие....
2 - Отгадайте ,учится,пишет-кто вкусный,сочный,алый-что...
2 - Кто совершил первое кругосветное плавание...
1 - Составить уравнение плоскости проходящей через точки а(-3; 2; 1) и в(4;...
3 - Вставить пропущенное слово: на берегу озера сидели рыбаки и...
1 - 1)чтобы вычислить разность чисел 15,6 и 8,8, преобразуем её так,чтобы вычитаемое...
2 - Ирина и нина малы.поставить ударения...
3 - Составте портрет князя ярослава мудрого....
2 - Сторона ромба равна 15,а острый угол равен 60 градусов найдите длину меньшей...
3