1. Математика
  2. Найти площадь фигуры, лежащей

Найти площадь фигуры, лежащей в правой полуплоскости и ограниченной окружностью x^2+y^2=8 и параболой

Pomogite5pozalystaz Pomogite5pozalystaz    2   05.05.2020 21:42    0

Ответы
зулик3 зулик3  14.10.2020 07:51

x^{2} + y^{2} = 8 — уравнение окружности с центром (0; \ 0) и радиусом \sqrt{8}.

y^{2} = 2x — уравнение параболы

Изобразим графики данных уравнений и найдем площадь образовавшейся фигуры в правой полуплоскости.

Выразим ординаты данных уравнений:

y = \pm\sqrt{8 - x^{2}} и y = \pm\sqrt{2x}

Так как имеем симметричные фигуры, найдем площадь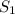 S_{1} одной из них. Общая их площадь 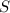S будет состоять из площади двух 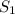S_{1}, то есть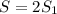 S = 2S_{1}

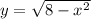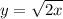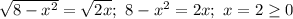
Тогда y =\sqrt{8 - x^{2}} и y = \sqrt{2x}. Поэтому \sqrt{8 - x^{2}} = \sqrt{2x}; \ 8 - x^{2} = 2x; \ x = 2 \geq 0

Так как окружность вытесняет больше площади, чем парабола, то имеем разность их площадей, определяющаяся через определенный интеграл:

S_{1} = \displaystyle \int\limits^{2}_{0} {\left(\sqrt{8 - x^{2}} - \sqrt{2x} \right)} \, dx = \int\limits^{2}_{0} {\sqrt{8 - x^{2}}} \, dx - \int\limits^{2}_{0} { \sqrt{2x} } \, dx

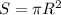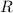Найдем первый интеграл геометрически: площадь круга находится по формуле S = \pi R^{2}, где R — радиус круга. Тогда четверть круга: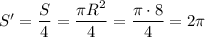 S' = \dfrac{S}{4} = \dfrac{\pi R^{2}}{4} = \dfrac{\pi \cdot 8}{4} = 2\pi

Найдем второй интеграл по формуле Ньютона-Лейбница:

\displaystyle \int\limits^{2}_{0} { \sqrt{2x} } \, dx = \dfrac{2\sqrt{2x^{3}}}{3} \bigg|_{0}^{2} = \dfrac{2\sqrt{2 \cdot 2^{3}}}{3} - \dfrac{2\sqrt{2 \cdot 0^{3}}}{3} = \dfrac{8}{3}

Таким образом,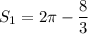 S_{1} = 2\pi - \dfrac{8}{3} кв. ед.

Тогда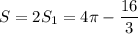 S = 2S_{1} = 4\pi - \dfrac{16}{3} кв. ед.

ответ: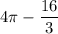 4\pi - \dfrac{16}{3} кв. ед.


Найти площадь фигуры, лежащей в правой полуплоскости и ограниченной окружностью x^2+y^2=8 и параболо
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
срочно118 срочно118  26.09.2019 00:20
Юра проплыл 30м со скоростью15м/мин,а витя за это же время проплыл 40 м.с какой скоростью плыл витя...
Dddgirl777 Dddgirl777  26.09.2019 00:20
9роз и 10 хризантем стоят 888 рублей. какова цена каждого цветка, если роза в 3 раза дороже хризантемы? напишите пояснение к первому действию и ко второму действию: 1)9•3=27(...
NoraDun NoraDun  26.09.2019 00:20
((2х-6)-3)*2=3 раскройте скобки . решать не надо☝...
lika343 lika343  26.09.2019 00:20
Только в столбик пож. 768 / 24,,966 / 32 ,,2814 / 67 ,,867720 / 42,, 91375 /43,,20944 /56...
Popop11hs Popop11hs  26.09.2019 00:20
2. мужчина упал с площадки автопогрузчика, ударившись грудью о твердый предмет. сильная боль в груди, дыхание поверхностное, частое. боль усиливается при кашле и изменении...
Adalet555 Adalet555  26.09.2019 00:20
Реши уравнение 640 минус икс равно 100 умножить на 3...
agent687p0bqk2 agent687p0bqk2  26.09.2019 00:20
Пациенту назначено введение 2,4л раствора внутривенно в сутки.рассчитайте скорость инфузии,если известно,что 1мл жидкости равен 20 каплям....
raxievali raxievali  26.09.2019 00:20
Первые 3 часа автомобиль ехал со скоростью 50 км в час следующие полчаса со скоростью 100 км.час а затем 2 часа со скоростью 75 км в час найдите среднюю скорость автомобиля...
KarenXacul80 KarenXacul80  26.09.2019 00:20
Найдите значение выражения: (3 2/3 - 1 2/7 * 5 4/9) : (-2.5)...
pukan03424 pukan03424  26.09.2019 00:20
Со склада продали в первый день 15,6ц картофеля, во второй день на 30 % больше, чем в первый, а в третий день на 25% меньше, чем в первый и второй день вместе. сколько...

Популярные вопросы