1. Математика
  2. .Найти первообразную

.Найти первообразную функции f (x) = х^2 + 6, график которой проходит через точку А (3;1).

marimuravskap08uv0 marimuravskap08uv0    3   08.06.2020 14:29    0

Ответы
Kutisheva2006 Kutisheva2006  15.10.2020 13:24

F(x) = \frac{x^3}{3} +6x-26.

Пошаговое объяснение:

1) За правилами интегрирования находим первообразную от f(x):

f(x)=F(x)=\frac{x^3}{3} +6x+C.

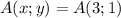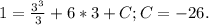
2) A(x;y)=A(3;1), то есть: 1=\frac{3^3}{3} +6*3+C; C=-26.

3) Итого имеем первообразную, которая проходит через точку А (3;1):

F(x) = \frac{x^3}{3} +6x-26.


.Найти первообразную функции f (x) = х^2 + 6, график которой проходит через точку А (3;1).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
gsgshhshsbababa gsgshhshsbababa  11.08.2019 03:20
Вклассе 40 человек. из них 26 человек играют в баскетбол, 25 занимаются плаванием, 27 ходят на лыжах. одновременно занимаются плаванием и баскетболом 15 человек, баскетболом...
timurtim1 timurtim1  11.08.2019 03:20
С! число диагоналей многоугольника на 12 больше числа его сторон. сколько сторон у этого многоугольника?...
azizka4 azizka4  11.08.2019 03:20
Найди значение выражений (272072: 8+181044: 9)•3-282126: 6...
Dmytro19 Dmytro19  11.08.2019 03:20
Если x=1.5 4(6-7x)+7(4x-5)=-11 если x=0 4(x-0.5)-2(x+0.3)=-2.6...
Виталина111111111111 Виталина111111111111  11.08.2019 03:20
Решите с вопросами книга дороже тетради в 5 раз. за книгу и тетрадь заплатили 120 руб. сколько всего нужно заплатить за 4 такие тетради и 3 такие книги?...
msekater97 msekater97  11.08.2019 03:20
Одна сторона прямоугольника 12см, а другая на 5 меньше.выясните отношение сторон прямоугольника....
vasili6513 vasili6513  11.08.2019 03:20
Сколько будет 2+2? в шестнадцатеричной системе счисления....
mzachinyaeva mzachinyaeva  11.08.2019 03:20
Прочитай формулировки и скажи, что в них общего. 1. миша нашел 5 белых грибов, а маша - 7. на сколько больше белых грибов нашла маша, чем миша? 2. в красной коробке...
ВеселыйР0джер ВеселыйР0джер  11.08.2019 03:20
Найдите сумму всех целых чисел, удовлетворяющих неравенству -27,98...
Дарья8402 Дарья8402  11.08.2019 03:20
Периметр треугольника равен 97 с одна сторона -а см вторая б см . составьте вырожение для нахождения третьей стороны. вычислите длинну третьей стороны, если а =32 б=26...

Популярные вопросы