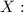Найти ожидание для значения X, распределенного непрерывно с плотностью
f (x) = 12 * (x * x - x * x * x) для x лежащих (0,1) и f (x) = 0 в других точках
Другие вопросы по теме Математика
Популярные вопросы
- Корень из х-2=х-4 как называется это уравнение?...
1 - План по рассказу стрижонок скрип 4 класс...
3 - При равновесии рычыга на его меньшее плечо действует сила 500h.меньшее...
3 - Разбор слова как часть речи: рассматривая...
3 - Соедини приставки, корни, суффиксы и окончания так, чтобы получились...
2 - Примеры на увеличение и уменьшения силы трения...
2 - Укажите бессоюзные сложные предложения, между которых ставится тире (знаки...
2 - Сравните сказку евгения шварца два брата и сказку снежная королева 40...
2 - 1) выполните действия а. 1) 11101001+10011101 2)11001011+11011011 б....
3 - Сочинение почему нужно любить читать...
2
Математическое ожидание непрерывной случайной величины