1. Математика
  2. Найти ординату точки ближайшей

Найти ординату точки ближайшей к точке А(-9/2;0)и лежащей на кривой у= корень -х

БЛОБ БЛОБ    3   03.08.2020 17:05    4

Ответы
UskovaV99 UskovaV99  15.10.2020 15:40

A\left(-\dfrac{9}{2} ;\ 0\right)

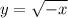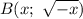Выберем на кривой y=\sqrt{-x} некоторую точку B(x;\ \sqrt{-x} ).

Найдем расстояние АВ:

AB=\sqrt{\left(-\dfrac{9}{2} -x\right)^2+(0-\sqrt{-x} )^2}

AB=\sqrt{\left(\dfrac{9}{2} +x\right)^2+(\sqrt{-x} )^2}

AB=\sqrt{\dfrac{81}{4} +9x+x^2-x}

AB=\sqrt{x^2+8x+\dfrac{81}{4}}

Так как необходимо найти ближайшую точку В к точке А, то расстояние АВ должно быть минимальным.

Найдем при каком значении х функция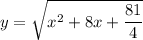 y=\sqrt{x^2+8x+\dfrac{81}{4}} принимает наименьшее значение. В силу того, что функция корня принимает наименьшее значение при наименьшем аргументе, это произойдет, когда аргумент 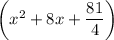\left(x^2+8x+\dfrac{81}{4}\right) примет наименьшее значение. Значит, нужно найти, при каком значении х функция 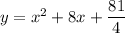y=x^2+8x+\dfrac{81}{4} принимает наименьшее значение. Выделим полный квадрат:

x^2+8x+\dfrac{81}{4}=(x^2+8x+16)-16+\dfrac{81}{4}=(x+4)^2+\dfrac{17}{4}

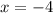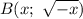При x=-4 расстояние АВ будет наименьшим. Значит, ордината точки B(x;\ \sqrt{-x} ) равна:

y=\sqrt{-x} =\sqrt{-(-4)} =\sqrt{4} =2

ответ: 2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
TvaylatHale123 TvaylatHale123  10.03.2019 13:50
Ювелиру принесли 4 обрывка браслета по 3 звена в каждом, и попросили починить браслет. ювелир выполнил заказ раскрыв только 3 звена. как он это сделал?...
LonelyFox1705 LonelyFox1705  10.03.2019 13:50
Решить . ковер-самолёт за 4 часа может пролететь 720 км. какое расстояние он пролетит за 6 часов с той же скоростью?...
CrazyMashin CrazyMashin  10.03.2019 13:50
На путь от села до пристани велосипедист затратит 0,4 ч,если будет ехать со скоростью 12,6км\ч.сколько времени затратит на этот путь пешеход,если будет идти со скоростью 4,2 км\ч?...
Lizasuper2003 Lizasuper2003  10.03.2019 13:50
Найдите значение выражения: 21/8 умножить на (6/7-2/3) подскажите как решить ....
rushsh1 rushsh1  10.03.2019 13:50
При обработке 80т риса получили 60г крупы.найти: %выхода крупы при обработке риса....
Stepka112 Stepka112  10.03.2019 13:50
Коли з сулії відлили декілька літрів олії, то в ній залишилось 14 літрів олії. скільки літрів було в сулії?...
katuxa65789 katuxa65789  10.03.2019 13:50
Напишите все двузначные числа которые являются кратными 25...
chobanu81p08xbb chobanu81p08xbb  10.03.2019 13:50
Число десятков на 5 меньше числа единиц,а число сотен на 6 меньше числа единиц, решение...
bcfujd19 bcfujd19  10.03.2019 14:00
Скільки різних трицифрових чисел. усі цифри яких різні. можна написати цифрами. а) 1 2 і 3. б)2 3 і 8....
DedPerdun DedPerdun  10.03.2019 14:00
Вдвух мешках 115.92 кг муки.в одном из них муки. в одних из них муки 1.3 раза меньше,чем в другом.сколько килограммов муки в каждом мешке...

Популярные вопросы