Найти общий интеграл дифференциального уравнения (1+e^x)*y’=y(e^x)

ответ: y/(1+eˣ)=C.

Пошаговое объяснение:

Перепишем уравнение в виде (1+eˣ)*dy/dx=y*eˣ. Это уравнение с разделяющимися переменными, которое приводится к виду dy/y=eˣ*dx/(1+eˣ), или dy/y-d(1+eˣ)/(1+eˣ). Интегрируя обе части, получаем ln(y)-ln(1+eˣ)=ln(C), или y/(1+eˣ)=C.

Проверка:

y=C*(1+eˣ), y'=C*eˣ, (1+eˣ)*C*eˣ=C*(1+eˣ)*eˣ. Так как получено тождество, то решение найдено верно.

ответ:   .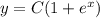

Пошаговое объяснение: