Найти общий интеграл дифференциального уравнения (1+e^x)*y’=ye^x
Другие вопросы по теме Математика
Популярные вопросы
- Міністерство оборони україни внесло у верховну раду в порядку законодавчої...
3 - Выполните действие 5дм+30см-120мм а)6дм 8см б)70см в)6дм г)80см...
3 - Складіть діалог-розпитування(4-5 реплік) використавши-дев яносто...
3 - Вправильной четырехугольной пирамиде mabcd тангенс угла наклона...
2 - Кто нибудь объясните как решать к примеру 2/3 из 21 примеры. объясните...
3 - Сочинение миниатюра встречали ли вы в жизни мужественных героев...
2 - Винаходи середньовіччя і вплив винаходів на серендньовічнє суспільство...
1 - Какое кол-во теплоты получает 2кг. гелия при изохорном нагревание...
3 - Назовите , которые были популярны у нашего народа в древности...
1 - Генотип женщины аавв а) 2 типа гамет: ав, ав б) 4 типа гамет: ав,...
2
ответ: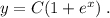
Пошаговое объяснение:
Решение на листочке ===>>