1. Математика
  2. Найти общие решения дифференциального

Найти общие решения дифференциального уравнения второго порядка: y//=xsinx;

Masha6996 Masha6996    1   25.09.2019 11:00    1

Ответы
DmitriyKefir DmitriyKefir  08.10.2020 18:15
Дважды почленно проинтегрируем левую и правую части уравнения, получим

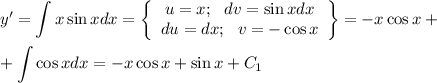
y'=\displaystyle \int x\sin xdx= \left\{\begin{array}{ccc}u=x;~~ dv=\sin xdx\\ du=dx;~~ v=-\cos x\end{array}\right\}=-x\cos x+\\ \\ +\int \cos x dx=-x\cos x+\sin x +C_1

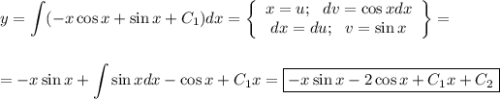
y=\displaystyle \int (-x\cos x+\sin x +C_1)dx= \left\{\begin{array}{ccc}x=u;~~ dv=\cos xdx\\ dx=du;~~ v=\sin x\end{array}\right\}=\\ \\ \\ =-x\sin x+\int \sin x dx-\cos x+C_1x=\boxed{-x\sin x-2\cos x+C_1x+C_2}
ПОКАЗАТЬ ОТВЕТЫ
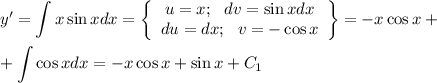
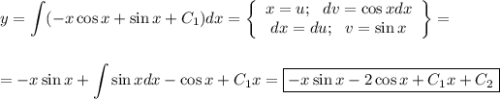
Другие вопросы по теме Математика
diksimail diksimail  07.04.2020 11:56
Два самолёта вылетели из аэропорта в противоположные стороны.Через 50мин. между ними было 8000км. С какой скоростью летел первый самолет если второй летел 100км/ч...
straza982 straza982  07.04.2020 11:56
5. При делении натурального числа п на 9 внеполном частном получается Ќ, а востатке 3. Укажите формулу зависимостимежду пи К.А) n=9k+3В) k=9n+3C) n=9k-3D) k=9n-3​...
хочусдохнуть хочусдохнуть  07.04.2020 11:56
Напишите верно или неверно данное утверждение. 1% от 100 это 1 1% от 400 это 40 1% от 5000 это 5 1% от 250 это 0,25 1 % от 1000 это 100 1 % от 1500 это 15 1 % от 1600...
0304131 0304131  07.04.2020 11:56
Доместости при35Г. Объясни правописание подчёркнутых букв.​...
nusuperirish nusuperirish  07.04.2020 11:56
Дам 30 б РЕШИТЕ ДАННЫЕ ПРИМЕРЫ...
Al2017 Al2017  07.04.2020 11:56
1) 107; 122; 113; 2) 12,4; 14,8; 18,9; 20,1; 3) 11; 17,2; 20; 24,6; 4) 0,89; 1,23; 1,64; 1,79; 2....
DeathStroke11 DeathStroke11  07.04.2020 11:56
Укажите верное соотношение для множеств А = {3, 4, 7, 8}, В = {4, 8, 10, 12}, С = {3, 4, 5, 6, 7, 8} 1. А с С 2. С с В 3. В с А 4. А с В С объяснением...
Pravednick Pravednick  07.04.2020 11:56
Разложите на множители 64 - (b+1)2...
slaider1123 slaider1123  07.04.2020 11:56
Сравни. Выбери знак , или = 5 м² 5000 см² 200 дм² 2 м² 680 см² 8 дм²...
1234Носок 1234Носок  07.04.2020 11:56
В сборнике билетов по физике всего билетов, в восьми из них встречается во по оптике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику...

Популярные вопросы