Найти общее решение (общий интеграл) дифференциального уравнения второго порядка - x (y"+1)=-y'

Пошаговое объяснение:

Это уравнение допускает понижение порядка с следующей замены: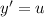

Это неоднородное линейное уравнение. Его общее решение можно представить в виде суммы общего решения однородного уравнения и частного решения неоднородного: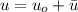

Рассмотрим однородное уравнение:

Частное решение неоднородного уравнения имеет смысл искать в виде: :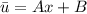

То есть общее решение есть: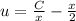

Возвращаемся к замене: