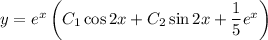Найти общее решение ЛНДУ 2 порядка с постоянными коэффициентами решить сам никак
Другие вопросы по теме Математика
Популярные вопросы
- Казакстан кандай ел?сочинение 50-70 слов...
1 - ІВ ДУЖЕ ТРЕБА! складіть хронологічну таблицю основних подій міжнародних відносин...
2 - ПОМАГИТЕ РЕШИТЬ ЗАДАЧИ БУДУ ОЧЕНЬ БЛОГОДАРЕН 1 тело объемом 3600 см3погружено...
3 - Закончить уравнения химических реакций, в уравнении 4 определить окислитель...
3 - РЕШИТЬ Длина ребра куба ABCDA1B1C1D1 1)равна 1. Вычислите скалярное произведение...
2 - Choose the right verb form: Present Simple or Past Simple. 1. Mum always (cooks/cooked)...
1 - Расскажите, на какие разряды по значению делятся союзы. Перечислите сочинительных...
2 - Роль живых организмов в экосистеме...
3 - Определите направление биологического прогресса у организмов: клест-сосновик,...
3 - Який шлях розвинуту подій окреслюється в новелі Останній листок?До ть...
1
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является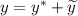 .
.
1)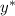 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену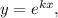 где
где 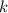 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 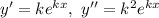
Получили характеристическое уравнение:
Разделим обе части уравнения на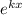 :
:
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда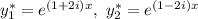
Воспользуемся формулой Эйлера: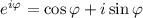
Фундаментальная система решений: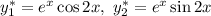 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 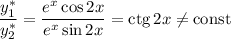
Общее решение: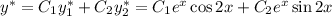
2)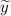 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 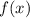 .
.
Здесь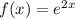 , причем
, причем 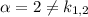 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 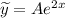 , где
, где 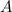 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда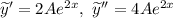 и
и 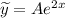 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 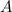 :
:
Разделим обе части уравнения на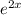
Таким образом, частное решение: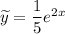
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
ответ: