Найти общее решение линейного неоднородного дифференциального уравнения методом неопределенных коэффициентов. у" +25у = 100xsin5x+50cos5x необходимо указать корни характеристического уравнения, вид частного решения линейного неоднородного дифференциального уравнения (с неопределенными коэффициентами).
Другие вопросы по теме Математика
Популярные вопросы
- Примерное меню древнего бедного римляна...
1 - Составьте рассказ от лица древнего римляна. и кратко, : * , 5 класс...
1 - Проверочные слова к: использовать-букву вторую ( о) жаловаться-букву первую (о)...
1 - Скласти та записати розповідь про те як треба поводитися у гостях, використовуй...
1 - При каких значениях k и b прямая y=kx+b проходит через точки a(1 ; 8) и b(-1...
1 - Втрапеции abcd ab=cd ac=5 ch=3 найти площадь...
2 - Составьте предложение со словом туда употребив его или в роли несогласованного...
3 - Найдите обьединение и пересечение множеств: а) n и z б) n и q в) z и q...
2 - Сообщение на тему: театр музыкальной комедии...
3 - Защита населения от чрезвычайных ситуаций.комплекс мер,проводимых по защите населения.организация...
1
Найдем сначала общее решение соответствующего однородного уравнения:
Пусть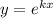 , получим характеристическое уравнение:
, получим характеристическое уравнение:
Характеристическое уравнение имеет два комплексных корня Два линейно независимые решения это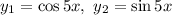
Общее решение однородного дифференциального уравнения:
Рассмотрим правую часть дифференциального уравнения:
Число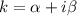 принимает значение
принимает значение 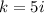 , это число является корнем характеристическое уравнение
, это число является корнем характеристическое уравнение 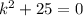 . Кратность k=1
. Кратность k=1
Частное решение будем искать в виде:
Вычислим для нее производную второго порядка
Подставив в исходное дифференциальное уравнение, получим:
Приравниваем коэффициенты при xcos5x, xsin5x, sin5x, cos5x, получим систему уравнений:
Частное решение: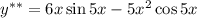
Общее решение линейного неоднородного дифференциального уравнения: