Найти общее решение (интеграл) дифференциального уравнения
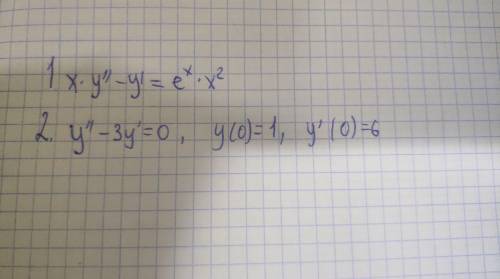
Другие вопросы по теме Математика
Популярные вопросы
- (Земля и Спутник Луна) Выбери Вариант высказывание, соответствующиц иллюстративному...
1 - 2. Каков порядок расположения лучей в спектре? 3. Почему ширина спектра зависит...
1 - 2.Скласти доповідь на тему Службові частини мови...
2 - 7. Төл сөз бен автор сөзін қатыстырып, «Туған табиғатқа саяхат» тақырыбында шағын...
2 - • Как относится Берендей к своему народу? Почему вы так считаете? • Какие пороки...
1 - використовуючи основну властивість пропорційної розвяжи рівняння 0.8 - х/ 2 =...
3 - ❗️ Задание 1 Скорость автомобиля равна v = 15 км/ч. Найдите путь, который автомобиль...
2 - 1. Ідеєю оповідання «Білий кінь Шептало» є А захоплення прагненням особистості...
3 - A) x + y = 4;6) 2x - y = 2;B) x + 2y = 4;D) x - y = 0...
1 - 2 Read the text again to find the numbers below. What does each number refer...
3
1)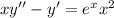
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на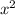 , получаем
, получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл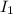 по частям.
по частям.
2)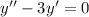
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена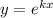 , перейдём к характеристическому уравнению:
, перейдём к характеристическому уравнению: 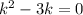 ,
, 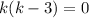 корни которого
корни которого 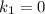 и
и 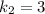 . Тогда общее решение диф. уравнения:
. Тогда общее решение диф. уравнения: 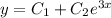 и его первая производная
и его первая производная 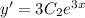 .
.
Осталось найти константы C₁ и C₂ , подставляя начальные условия.