Найти общее решение дифференциального уравнения y"+9y=9/sin3x
Ответы
Дифференциальное уравнение 2-го порядка
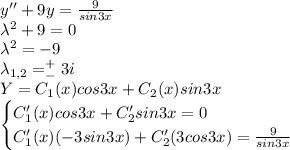
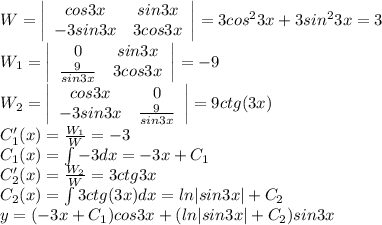
ПОКАЗАТЬ ОТВЕТЫ
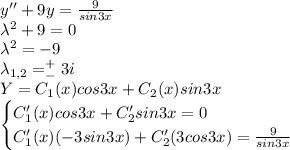
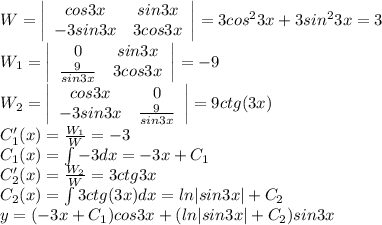
Другие вопросы по теме Математика
Популярные вопросы
- ЗАДАНИЕ НЕ СЛОЖНОЕ. 644. 1. Придумайте и запишите сложноподчинён- кые предложения,...
1 - Вариант 6 1. Напряжение на участке AB (рис. 100) равно 100 В, а силатока...
3 - Синонимы к слову свобода на казахском языке...
3 - Чему равен х и у? Покажите как решили...
1 - Сколько подписчиков у ВладаА...
1 - Решите примеры А) 7(х-1)-12=30 Б) 3(х-8)=4х-9 В) 10х-2(4х-1)=19...
1 - При температурі 16° в приміщенні точка роси 6°. Визначити відносну вологість...
2 - 4. Суреттегі көлік түрлерін атқаратын қызметіне қарай топтастырыңдар. Қандай...
1 - Проанализируйте постановление Пленума Верховного Суда РФ от 27.09.2012...
3 - Найдите словосочетание с действительным причастием 1) написанная учеником...
1