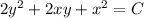Найти общее решение дифференциального уравнения
(x+y)dx+(x+2y)dy=0
Другие вопросы по теме Математика
Популярные вопросы
- написать что сделали Амир Хайдар(1800-1826) и Амир Насрулла(1836-1860)...
3 - Чого павла називали павлентієм з твору вогник далеко в степу?...
2 - ВЫПИШИТЕ СЛОВА КОТОРЫЕ УКАЗАНЫ В МНОЖЕНСТВИНОМ ЧИСЛЕ КАЗАХСКИЙ ЯЗЫК...
3 - Ребята нужна характеристика Осипа по плану: 1)говорящая фамилия 2)поступки...
2 - Что нужно для полетение космоса...
3 - 1) Греческая цивилизация зародилась ок. до н.э. 2) Ранний зэтап греческой...
1 - Дан прямоугольный треугольный треугольник. Катет BC меньше катета...
2 - Найдите в данных предложениях тропы (выразительные средства) и укажите...
1 - Выберите вещества хорошо растворимые в воде: натрий-гидроксид соляная...
2 - Кто может не чё не пойму??? Задача в первой бригата может выполнить...
1
Пусть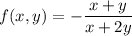
Тогда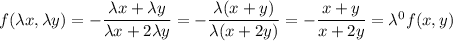
Имеем однородную функцию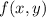 нулевого измерения.
нулевого измерения.
Положим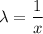 в
в 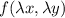 , то есть
, то есть 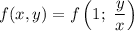
Тогда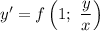 . Замена:
. Замена: 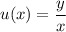 , откуда
, откуда 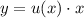 и
и 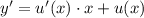
Здесь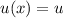 , тогда имеем уравнение:
, тогда имеем уравнение:
Обратная замена:
ответ: