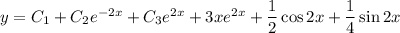Найти общее решение дифференциального уравнения, с пояснениями, если не составит труда
Большое Найти общее решение дифференциального уравнения, с пояснениями, если не составит труда Большое

— неоднородное дифференциальное уравнение третьего порядка с постоянными коэффициентами

Принцип суперпозиции решений

Общее решение такого уравнения: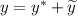 , где 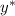— общее решение соответствующего однородного уравнения, 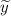— частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.

Метод Эйлера: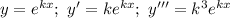

Характеристическое уравнение: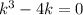

Фундаментальная система решений:

Общее решение: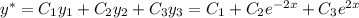

Здесь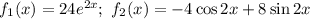  

Контрольные числа: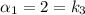 — является корнем характеристического уравнения; 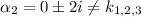— не является корнем характеристического уравнения;

Тогда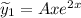 и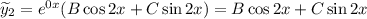

Находим неизвестные коэффициенты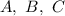 методом неопределенных коэффициентов:

Коэффициенты около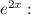

Коэффициенты около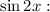

Коэффициенты около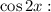

Таким образом,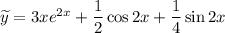

Общее решение заданного уравнения:

ответ: