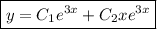Найти общее решение дифференциального уравнения. a)2y''+3y'+ y=0 б)y''+4y'+8y=0 в)y''-6y'+9y=0
Другие вопросы по теме Математика
Популярные вопросы
- Основа прямої призми-прямокутний трикутник з катетом 4см. і...
2 - Укажи, какой частью речи являются слова с данными окончаниями....
3 - 1. выражения: а) -3х(2-х)+(3x+1)(x-2) б) 3(2х-1)^2+12х в) (х+3)^2-(х-2)(х+2)...
3 - Найдите км в квадрате abcd по рисунку. все условия на изображении....
2 - Сравнить кинетическую энергию пули до соударения с кинетической...
1 - Определить массовую долю сахара в растворе, если к 200г воды...
3 - Скажите кросворд со словом на украинском 5 клас...
3 - Цена на товар была повышена на 23% и составила 2091 рубль. сколько...
2 - Вставить слова в предложениях (...
1 - (3 корня из 5-2 корня из 20) корень из 5 = ?...
3
а) Это однородное дифференциальное уравнение с постоянными коэффициентами. Перейдем к характеристическому уравнению, сделав замену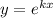
Решая как квадратное уравнение, получим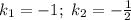
Общее решение: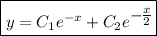
б) Дифференциальное уравнение второго порядка с постоянными коэффициентами, однородное.
Пусть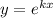 , получим характеристическое уравнение:
, получим характеристическое уравнение:
Общее решение: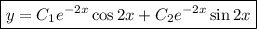
в) Пусть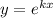 получим следующее характеристическое уравнение:
получим следующее характеристическое уравнение:
Общее решение: