1. Математика
  2. найти общее решение Дифференциального

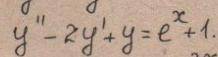
найти общее решение Дифференциального уравнения


найти общее решение Дифференциального уравнения

kristina05081999 kristina05081999    3   27.12.2020 16:30    0

Ответы
ооиррррр ооиррррр  26.01.2021 16:30

1) Решаем ОЛДУ:

y'' - 2y' + y = 0

замена:

y = {e}^{kx}

{k}^{2} - 2k + 1 = 0 \\ {(k - 1)}^{2} = 0 \\ k1 = k2 = 1 \\ y = C1 {e}^{x} + C2 {e}^{x} x

2) Подбираем у с неопределенными коэффициентами:

y1 = A

y2 = B{e}^{x} \times {x}^{2}

умножаем на х^2, так как в общем решении ОЛДУ два слагаемых с е^х.

y = A + B{e}^{x} {x}^{2}

y = B{e}^{x} {x}^{2} + 2Bx {e}^{x} = \\ = {e}^{x} (B {x}^{2} + 2Bx)

y = {e}^{x} (B {x}^{2} + 2Bx) + {e}^{x} (2Bx + 2B) = \\ = {e}^{x} (B{x}^{2} + 4Bx + 2B)

Подставляем в НЛДУ:

{e}^{x} (B {x}^{2} + 4Bx + 2B) - 2 {e}^{x} (B { x}^{2} + 2Bx) + A + B {e}^{x} {x}^{2} = 1 + {e}^{x} \\ {e}^{x} (B {x}^{2} + 4Bx + 2B - 2B{x}^{2} - 4Bx + b {x}^{2} ) + A = 1 + {e}^{x} \\ 2B {e}^{x} + A = {e}^{x} + 1

Отсюда:

A = 1

2B = 1 ; B = 1/2

Получаем:

y = 1 + \frac{ {x}^{2} }{2} {e}^{x} \\

общее решение:

y = C1 {e}^{x} + C2 {e}^{x} x + 1 + \frac{ {x}^{2} {e}^{x} }{2} \\

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
bekkalvina2405 bekkalvina2405  20.07.2019 05:30
Начертите прямую а изобразите такие точки к lm чтобы расстояние от точки к до прямой а равнялось 2 см.от точки l до прямой а-4,3см и от точки м до прямой а -3,1см...
Babikovandrei48 Babikovandrei48  20.07.2019 05:30
Втреугольнике abc угол b в 4 раза,а угол c в 7 раз больше угла a.найдите все углы треугольника abc...
Nikita45Russia Nikita45Russia  20.07.2019 05:30
Надо решть с уравнения : чтобы во время вернуть учебник в библиотеку, ученик ежедневно должен прочитать по 40 стр. но каждый день он читал по 15 стр. и поэтому он вернул книгу на...
temachbatman temachbatman  20.07.2019 05:30
Купили 5 булочек и 3 пирожных по одинаковой цене. за булочки заплатили 20 рублей. сколько стоят пирожные?...
Stasikone Stasikone  20.07.2019 05:30
Запишите дробь в виде суммыдвух дробей а) три пятых,б)семь девятых,в)пять седьмых,г) три десятых...
lera978 lera978  20.07.2019 05:30
Какая площадь участка есть большей , 400кв.м, 14а, 4га....
mag792 mag792  20.07.2019 05:30
При пересечения двух прямых один из полученных углов равен 1) 75° 2) 120°. найдите градусные меры остальных углов...
Msirinaaa Msirinaaa  20.07.2019 05:30
Сравни. 9 км720м 972м 8420ц 84т2ц 4520см 45м2дм 180мин 2ч50мин 12т250кг 12350кг 360кг820г 36820г 4ц 400кг 360дней 1год 7м4дм 704см...
DevilingKeks DevilingKeks  20.07.2019 05:30
Округлите каждое из чисел до десятых 54,38709; 532,344453; 93,5959...
glebsemenov86 glebsemenov86  20.07.2019 05:30
Какую часть число, равное три седьмых от 21, составляет от числа, три пятых которого равны 15?...

Популярные вопросы