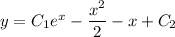Найти общее решение диф. уравнения понизив его порядок: y"-y'-x=0
Другие вопросы по теме Математика
Популярные вопросы
- Уклеток каких живых организмов вокруг плазматические мембраны клеточной...
1 - Построить график функций y=x^2-2x-3...
2 - Перевести на .: посмотри! это известный музыкант! ты узнаешь его?...
2 - Что играет главную роль в половом процессе инфузории?...
3 - Раскрыть скобки в правильном времени many,many years ago their (to...
3 - Сояинение про любимый урок в школе про язык 8 предложений (на )...
1 - Представьте в виде десятичных дробей дроби 4/5; 8/25; 1/4; 3/50;...
3 - Обозначьте падеж имён сущ землю огороде уборке урожая комбайн брошюре...
3 - Рассказ о картине в.васнецова царевна-лягушка...
2 - Для купили голубые и белые блесны в одинаковых коробках. оказалось,...
3
Пусть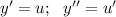 , получим:
, получим:
Умножим левую и правую части уравнения на множитель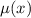 :
:
Интегрируя обе части уравнения, получим
Выполним обратную замену:
ответ: