Найти общее (частичный) решение уравнения.
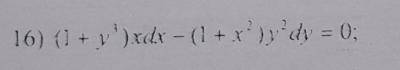
Другие вопросы по теме Математика
Популярные вопросы
- Для вещества с-сн3-с-с-с составить формулы гомолога и изомера и назвать...
1 - нужна. Fill in the gaps with the following words and word combinations...
1 - ОПРЕДЕЛИ ПЛОЩАДЬ КВАДРАТА,ДЛИНА СТОРОНЫ КОТОРОГО РАВНЫ 4 СМ...
2 - Выпишите из текста предложения с модальными глаголами и переведите их....
1 - 5. Как можно назвать переменную? A) goto Б) null В) true Г) const Д)...
1 - Какова индуктивность соленоида, если при силе тока 5 А, через него проходит...
2 - НАДО, ЛЮДИ ДОБРЫЕ, УМНЫЕ В восьмом вопросе там а) конкретная. Плохо видно....
2 - 1)Сума довжин усіх бічних ребер прямокутного паралелепіпеда дорівнює...
3 - Определите концентрацию раствора, если для его приготовления было израсходовано...
2 - 2р12-q12-2p12p-q при p=16q=9 Упростить и вычислить значение выражения...
1
общее решение