Найти область сходимости степенного ряда
решить
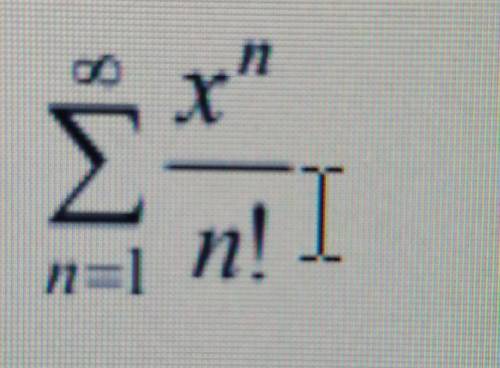
Другие вопросы по теме Математика
Популярные вопросы
- Сторони трикутника 29 і 25 і 6 см! знайти площу трикутника, радіус...
1 - Вася катал иру на качелях. подчеркнуть согласные твердые...
2 - Схема реакций , соответствующая сокращенному молекулярно-ионному уравнению...
2 - Векторы а и b параллельны,найти значение p,если вектор а(р; -6) и...
3 - Таволга таволга (полу)кустарник с крупными резными листьями. переб…ра…ш…ся...
2 - При каких значениях переменной не определена функция y=x-2/x^2-9 а)2;...
3 - По площадь равностороннего треугольника равна 25 . найдите длину стороны...
1 - Маляру поручено покрасить стену. за час работы он покрасил 21,6 метров...
3 - Представь числа 781 905 160 и 347 в виде суммы разрядных слагаемых...
2 - Переводчика.mr jones was very angry with his wife, and she was very...
1
Для этого используем формулу радикального признака Коши. В данном случае, у нас есть степенной ряд ∑ from n=0 to ∞
an(x-a)n.
Согласно радикальному признаку Коши, область сходимости степенного ряда можно найти следующим образом:
- Построим пропорцию и подберем значение для "a", чтобы пропорция стала верной:
|
| |
| |
| |
| |
| |_____________(a-r)
|
|
|
(0─a───────────r─∞)
- Затем нужно проверить сходимость ряда при значении а - r и при а + r.
- Если ряд сходится при а - r и при а + r, то его область сходимости будет отрезком (а-r, а+r).
- Если ряд сходится только при а - r, то его область сходимости будет (-∞, а+r).
- Если ряд сходится только при а + r, то его область сходимости будет (a-r, +∞).
- Если ряд сходится и при а - r, и при а + r, то его область сходимости будет (-∞, +∞).
Перейдем к решению задачи. У нас дан степенной ряд ∑ from n=0 to ∞ (3^n (x-4)^n)/5^(2n).
Применим радикальный признак Коши:
(3^n (x-4)^n)/5^(2n) > 0, так как является произведением положительных слагаемых.
Δ(1/n * ln |(3^n (x-4)^n)/5^(2n)|) = Δ(1/n * (ln(3^n) + ln((x-4)^n) - ln(5^(2n)))),
где Δ - обозначает предел при n стремящемся к бесконечности.
Построим пропорцию:
(3^n (x-4)^n)/5^(2n) > 1, так как произведение положительных слагаемых всегда больше 0. Запишем неравенство без модуля для удобства вычислений.
ln(3^n) + ln((x-4)^n) - ln(5^(2n)) > ln(1).
После подстановки формул в неравенство, получим:
n(ln(3) + ln(x-4) - 2ln(5)) > 0.
Так как n > 0, то имеем:
ln(3) + ln(x-4) - 2ln(5) > 0.
Складываем логарифмы:
ln(3(x-4)/25) > 0.
Это неравенство выполняется только тогда, когда аргумент внутри логарифма больше 1.
3(x-4)/25 > 1.
Решаем неравенство:
3(x-4)/25 > 1,
3(x-4) > 25,
3x-12 > 25,
3x > 37,
x > 37/3.
Таким образом, мы определили, что степенной ряд ∑ from n=0 to ∞ (3^n (x-4)^n)/5^(2n) сходится при значениях x > 37/3. Областью сходимости является интервал (37/3, +∞).