Найти область сходимости степенного ряда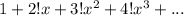

Буду благодарен если и объясните

Пошаговое объяснение:1+2!x+3!x²+4!x³+...=∑n!·xⁿ⁻¹

Степенной ряд в общем виде записывается следующим образом  : ∑aₙxⁿ, где an - формула числовых коэффициентов.

У нас   aₙ = n!

Областью сходимости степенного ряда является интервал (-R;R), где R - радиус сходимости, причём R=limₙ→∞ (aₙ /aₙ₊₁)

Найдём его: R=limₙ→∞  (aₙ /aₙ₊₁)= limₙ→∞ n!/(n+1)! =limₙ→∞ n!/n!(n+1)=limₙ→∞ 1/(n+1)=0

Итак, ряд является сходящимся (абсолютно) при всех x=0