Найти область сходимости функционального ряда/
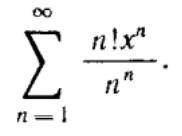
Другие вопросы по теме Математика
Популярные вопросы
- Какое природное явление, в конце XIII века Японию от вторжения иноземцев,...
3 - Чтение Задание Прочитайте тексты, выполните задания. 1. Сравните два текста,...
3 - Сравни с нулём: а) (-4,7)15 (это степень) ;(-1,001)100(это степень) ;(-5...
1 - C-CH4-C2H2-C2H4CL2-C2H4-CO2 Закінчити схему перетворень...
2 - Света купила 7 карандашей по цене x руб. за карандаш, а Таня купила 2 ручки...
2 - Дэнни мен Ривераны салыстырыныз мексика ұлы...
1 - За день рабочий изготовил 44 делали, что составляет 110% количества деталей,...
2 - Физики даю 10 , на странице будут еще во можете ответить , там побольше...
3 - Обозначить орфограммы в словах 1.намажьте 2.кое(с)кем 3.н… у кого не спрашивал...
2 - сделать морфологический разбор слов по казахскому Жауhар , Телегей...
3
выполняются, ряд расходится.
Область сходимости: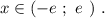
Пошаговое объяснение:
А тогда радиус сходимости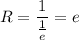
Исследуем сходимость на концах