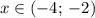Найти область сходимости функционального ряда
Другие вопросы по теме Математика
Популярные вопросы
- Коефіцієнт пружності пружини дорівнює 600 Н/м. На скільки треба стиснути пружину,...
2 - Встановіть відповідність між оксидом і основою, кислотою , амфотерним гідроксидом,...
3 - Мне её здавать черезь 20 минут...
2 - Розбір займенника скільки...
2 - О чем ты будешь вспоминать, увидев на улице собаку? (по повести Д.Пеннака «Собака...
2 - Решите Решением неравенства 0∙х 0 является:...
2 - В зеркале воды отражаются звёзды и тонкий серп месяца....
1 - 2. Слитно или раздельно? Докажи.1) За это кресло заплатили в два раза дороже, чем...
2 - А 3. В каком ряду пропущенные согласные не проверяются? 1) грус.. .ный, прелес.....
2 - Рассчитайте хватит ли водорода образовавшегося при взаимодействии 20 грамм уксусной...
1
Функциональный ряд имеет вид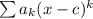 . Приведем наш ряд к такому виду.
. Приведем наш ряд к такому виду.
Ряд содержит лишь четные степени (x+3), а значит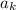 при нечетных
при нечетных 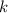 можно взять равными 0. Т.е.
можно взять равными 0. Т.е. 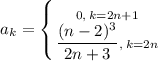
Последовательность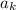 не имеет предела при
не имеет предела при 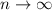 , а значит необходимо использовать формулу Коши-Адамара.
, а значит необходимо использовать формулу Коши-Адамара.
Заметим, что последовательность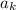 можно разбить на две подпоследовательности с конечными пределами, выделив нулевую подпоследовательность.
можно разбить на две подпоследовательности с конечными пределами, выделив нулевую подпоследовательность.
Тогда![\overline{lim}_{k\to \infty} \sqrt[k]{a_k}=\left [ MAX:\left \{ {{lim_{n\to \infty}\sqrt[2n+1]{0}=0} \atop {lim_{n\to \infty}\sqrt[2n]{\dfrac{(n-2)^3}{2n+3}}=1}} \right. \right ]=1=R=\dfrac{1}{\overline{lim}_{k\to \infty} \sqrt[k]{a_k}}=1](/tpl/images/1046/9024/56884.png)
Значит при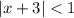 ряд сходится.
ряд сходится.
Исследуем сходимость на концах.
Если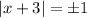 , получаем ряд
, получаем ряд 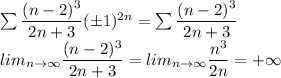 - необходимое условие сходимости не выполнено, значит ряд расходится.
- необходимое условие сходимости не выполнено, значит ряд расходится.
ответ: