Найти Область определения Д(y)
Область Значения Е(у)
Наибольшее и наименьшее значение функции
Нулифункции
Промежутки знака постоянства
f(x) >=0 f(x) <=0
Промежутки где функция возрастает и убывает
Другие вопросы по теме Математика
Популярные вопросы
- сочинение на тему tejamkor bolaylik ...
1 - На рисунке изображён график периодической функции y= f ( x), имеющей период...
2 - Найдите диагональ равнобокой трапеции с основаниям 7 см и 4 см и бок. Стороной...
2 - Составить алгоритм (план) устного ответа по теме Хозяйство семьи ...
1 - Определить степень окисления элементов в соединении. Назвать вещества. Br2O7;...
2 - Задание 4. Заменить данные словосочетания со связи управление синонимичными...
2 - На вход программы подаются оценки учеников 8 класса за контрольную работу по...
1 - Open the brackets using Future Simple. Write down 4 answers with a comma (,)....
3 - Две плоскости параллельны между собой через т. М, не лежащей ни в одной из этих...
3 - На пластинку падає світло з довжиною хвилі 400 нм. червона межа фотоефектту...
3
В решении.
Пошаговое объяснение:
Найти:
1) Область определения D(y);
2) Область значений Е(у);
3) Наибольшее и наименьшее значение функции;
4) Нули функции;
5) Промежутки знакопостоянства; f(x) > 0; f(x) < 0.
6) Промежутки где функция возрастает и убывает.
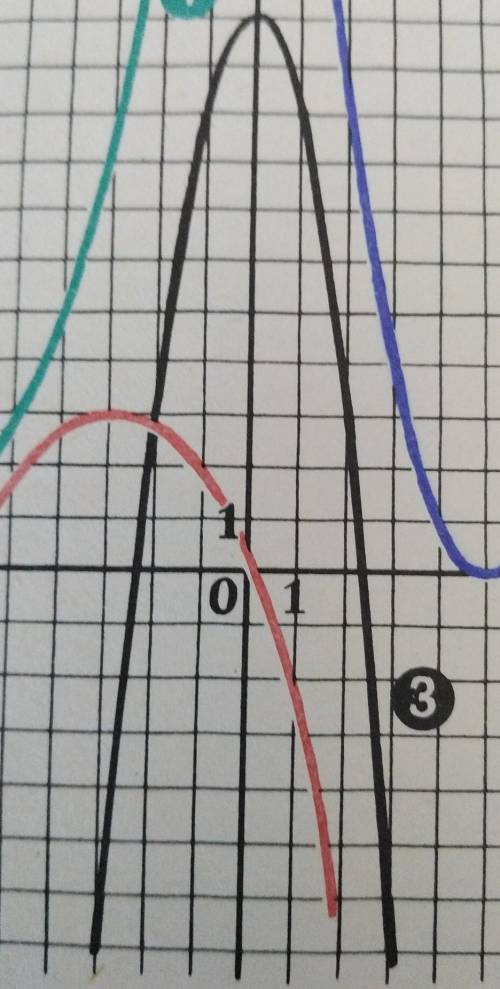
Дан график функции.
Квадратичная функция, график - парабола со смещённым центром, ветви направлены вниз, пересекает ось Ох при х = -2,3 и х = 2,3.
Координаты вершины параболы (0; 11).
1) Область определения D(y);
Область определения - это проекция графика функции на ось Ох.
Область определения параболы не ограничена ничем, потому что она проецируется на любую точку оси Ох.
Поэтому область определения - множество всех действительных чисел.
Запись: D(у) = R, или D(у): х∈(-∞; +∞).
2) Область значений Е(у);
Область значений - это проекция графика на ось Оу.
Область значений параболы ограничена координатами вершины, конкретно значением у вершины параболы.
Запись: Е(у) = у∈(-∞; 11].
3) Наибольшее и наименьшее значение функции;
У наиб. = 11;
У наим. не существует.
4) Нули функции;
Нули функции – это значение аргумента, при которых функция обращается в нуль. Точки, где график пересекает ось Ох.
Нули функции: х = -2,3 и х = 2,3.
5) Промежутки знакопостоянства; f(x) > 0; f(x) < 0.
Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна (не равна нулю).
f(x) > 0 (график выше оси Ох) при х∈(-2,3; 2,3),
f(x) < 0 (график ниже оси Ох) при х∈(-∞; -2,3)∪(2,3; +∞).
6) Промежутки, где функция возрастает и убывает.
Функция возрастает при х(-∞; 0).
Функция убывает при х∈(0; +∞).