Найти обе производные
задание на фото
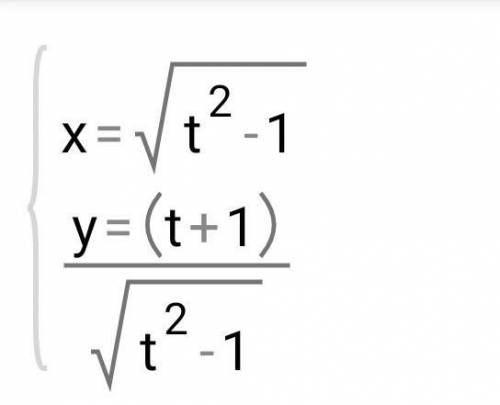
Другие вопросы по теме Математика
Популярные вопросы
- Задания суммативного оценивания за 4 четверть по предмету «Математика» 1. Определите...
2 - Хочу свою мать с чем это связано...
2 - Почему бактериальный инсулин также дешевле, чем химически синтезированный?...
1 - Тело растянуло в воздухе пружину динамометра с силой 88 Н, а в бензине — с...
2 - 1) как и почему Московская усобица замедлила объединение нашей страны во второй...
3 - 1. Продолжил традицию Коркыта, знаменитый кюши-композиторов, кобызист, автор...
3 - ответить на во Каковы функции и компетенция исполнительной власти? Какие условия...
2 - Укажи произведение Д.Свифта,...
2 - Контрольний твір Краса зовнішня і внутрішня Минимум на одну строничку...
2 - 1. Лось провалився під лід, тому що: А) втікаючи від вовків, вирішив перебігти...
2
Нужно найти производную параметрически заданной функции.
Формула: