Найти несобственный интеграл или доказать его расходимость:
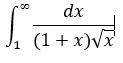
Другие вопросы по теме Математика
Популярные вопросы
- Как разобрать слово как часть речи моет...
3 - Определите, какие показатели относятся к сфере макро - , а какие...
3 - Запишите на языке.а) для того, чтобы умножить сумму на число,...
3 - 0,5^2 + 2^2 / 0,5^2 + 2^2 это можно сократить? или просто решать?...
3 - Наблюдатель оценили, что стае не меньше 40, но больше 50 птиц....
1 - Составьте числовое выражение и найдите его значение частное...
3 - Напишите где находится исток и устье рек обь, колорадо...
1 - Всем! вот задали написать сочинение на тему ( не поддавайтесь...
3 - Из списка слов выпишите сначала слова,используя которые необходимо...
1 - На малый поршень площадь которого 1м в квадрате действует сила...
1
Интеграл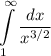 сходится, тогда сходится
сходится, тогда сходится 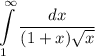 (по первому признаку сравнения).
(по первому признаку сравнения).
Второй вычисление определённого интеграла)