Найти неопределенный интеграл методом замены переменной
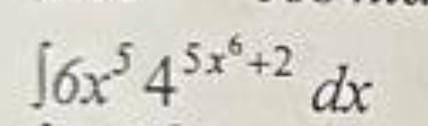
Другие вопросы по теме Математика
Популярные вопросы
- Раскройте скобки употребляя глаголы в Past Simple или...
1 - 1) Почему живые организмы рас на Земле неравномерно? 2) В каких...
2 - Вставьте окончания прилагательных: Зведн... небо, перв... полет,...
3 - (1)Помните, каким шумным был подмосковный лес весной и летом? (2)Теперь...
2 - При приближении магнита к кольцу в нем возникает ток. Как называется...
2 - Чехов Хамелион Выпишите из текста реплики, в которых проявляются...
3 - СКОРО ДОЛЖНЫ ОТПРАВИТЬ УЧИТЕЛЮ 1. Найди производный предлог1) Над2)...
3 - Тема писатели улыбаются журнал Сатирикон Всеобщая история обработанная...
3 - При каких значениях х значение зависимой переменной у= -0,5+4 равно...
1 - Какие организмы относят к консументам почему...
3
ответ: 1/5*4^(5*x⁶+2)/ln(4)+C.
Пошаговое объяснение:
Так как d(5*x⁶+2)=30*x⁵*dx, то ∫6*x⁵*4^(5*x⁶=2)*dx=1/5*∫4^(5*x⁶+2)*d(5*x⁶+2). Полагая u=5*x⁶+2, приводим данный интеграл к виду: 1/5*∫4^u*du. Это уже "табличный" интеграл, поэтому 1/5*∫4^u*du=1/5*4^u/ln(4)=1/5*4^(5*x⁶+2)/ln(4)+C.