Найти неопределённые интегралы
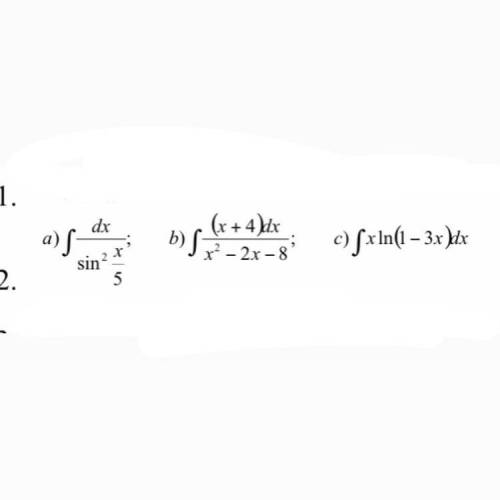
Другие вопросы по теме Математика
Популярные вопросы
- определить вид логической функции, которая будет соответствовать данной...
2 - с ребусом.последний ответ-нил...
1 - Есе на тему:Хто ми? Звідки ми? куди йдемо? ...
2 - В правильной треугольной пирамиде двугранный угол при ребре основания...
3 - Кратко расскажите о судьбе Маши Мироновой. В чём состоит её счастье...
2 - Нудно найти значение выражения....
3 - Представьте ионное соединение, образованное Al (13) и O (8), показав...
3 - Алтын адам Бірге жазылатын сөзді тап ...
1 - сравните конституцию и любой другой нормативный правовой акт российской...
2 - Часы, идущие по московскому декретному времени, показывают в Якутске...
3
в
б
В числителе делаем производную знаменателя
с
По частям: