Найти неопределенные интегралы.
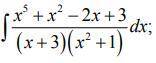
Другие вопросы по теме Математика
Популярные вопросы
- Я дослідив розвиток бруньок на пагонах...
3 - Дано точки A (1,2), B (4,6) , C (4,8) , D (1,4). З ясуйте , чи рівні вектори...
3 - Відсоткове відношення 2 і 10...
2 - Напишите уравнения реакций для осуществления превращений O2--K2O2--KOH--KClO3--O2...
1 - Как Санька относился к Саше и Тане Конь с розовой гривой ...
2 - Дано:a//b, c- секущая, уг1+уг2=102градуса.Найти: Все образовавшиеся углы....
3 - 1) Выполнить умножение: 1) (а – 7)(а + 7), 2) (6 + х)(х – 6), 3) (4в –...
2 - Запетання из земной поверхни...
1 - Запишите все дроби, равные 8/9, с числителями большими 30, но меньшими...
1 - составить предложение с too и enought по три предложения с too и ennought...
1
числитель больше знаменателя, выделим целую часть:
Разложим на простейшие дроби: