Найти неопределенные интегралы: 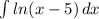
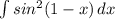
Другие вопросы по теме Математика
Популярные вопросы
- 1 At home, eat as much as I want. 2 At school, we talk in class.3...
3 - В чьому полягає особливості фірмового стилю масових заходів?...
3 - задания зависимостей между величинами: аналитический (с формулы),...
1 - Швидко вирішіть. -4,5(х-3)-1=7,2-5(х-2)...
1 - ОТ 1.Это удивительный вулкан, который возвышается среди открытого...
3 - 3. Державу Феодоро очолиладинастія.....
2 - 7. Почему считают, что только человек может заниматься де-ятельностью?...
2 - Дати відповідь на запитання «чи можу я бачити чари навколо себе?»...
1 - Сочинение описание По картине В.Репки ,,Водитель Валя (брать не...
2 - His brather had been treveling for a month Написать: общий, 2 специальных...
3
1)
решаем по частям:
2 .
воспользуемся формулой понижения степени