Найти наибольшее решение неравенства 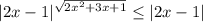
Другие вопросы по теме Математика
Популярные вопросы
- Выделите в данных словах окончания и основы. Укажите слова, которые...
3 - Знайдіть у себе дома 2-3 вимірювальні прилади що мають шкалу....
3 - Чем Византия как государство отличалась от стран Западной Европы?...
1 - 1 My dad 3 I think it4 Weon the eight o clock flight from Almaty...
2 - Проанализируйте вышеприведённые тексты. Заполните таблицу....
1 - Чому у міфах світ поділяється на протилежності: добро і зло...
2 - |х-15| + |х-18| -78 при х=7 надо, пишим ВПР...
1 - 1. Временное правительство пришло к власти после Февральской революции....
1 - Найдите радиус окружности с центром О, изображенной на рисунке....
2 - Як зробити паспорт пісні?До ть будь ласка...
1
(см. объяснение)
Пошаговое объяснение:
ОДЗ: x<=-1 или x>=-1/2.
С учетом ОДЗ:
Итого наибольший x, когда неравенство верно равен 1.
Задание выполнено!