Найти наибольшее и наименьшее значение функции.
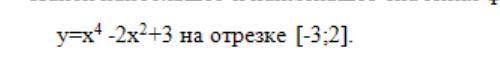
Другие вопросы по теме Математика
Популярные вопросы
- Розв яжіть задачі та запишіть відповідь у стандартному вигляді....
3 - Рочитай фрагменты из произведения К. Булычева «Сто лет тому вперед»....
3 - Соч по русскому литературе...
1 - Від поданих іменників утвори прикметники: Козак, Волга, Прилуки,...
3 - 1)Подумайте: окружающие все грустят, тебе тоже грустно, родным...
2 - Питання та завдання для самоконтролю та самостійної роботи: підібрати...
3 - Какая масса сульфата бария образуется при взаимодействии 32,6...
3 - 7. расскажите о последствиях походов Чингисхана...
2 - Можно ли использовать для образования сравнительной и превосходной...
1 - Площадь комнаты составляет 4×3=12м² Относительная влажность составляет...
1
Возьмём производную функции
y' = 4x^3-4x, приравняем ее к нулю
y'=0, 4x^3-x=0, x(x^2-1)=0, x(x-1)(x+1)=0
На числовой прямой: -[-1]+[0]-[1]+
Значит точки -1 и 1 точки локального минимума, точка 0 точка локального максимума. Так как функция четная(при замене х на -х функция остаётся такой же) возьмём значение х = 1. Тогда у=1-2+3 = 2. Возьмём х = 0. у=3. Проверим концы данного отрезка х = -3, у=66. х = 2, у = 11. Получаем, что наименьшее значение у=2, наибольшее у=66