Найти n. Если 25+27+29+(2n-1)=1456 подробное решение
Другие вопросы по теме Математика
Популярные вопросы
- НУЖНА СТРАНИЦА В ВК,НЕ В ТЕМУ(знаю),отдайте если кто-то может)...
3 - Диктант по теме Имя прилагательное выполнить задание по диктанту мне решить...
2 - Как решить? −2⋅(−1)⋅(−4)⋅(−4)...
2 - Установіть відповідність між прислівником та його творення сильно праворуч...
2 - График функции y = kx + b пересекает ось ординат в точке А (0; -4) и проходит...
3 - У выражение и найти его значение при а= -2: (а + 5)^2 – (а + 2)(а – 2)....
2 - Решите плз 0,1+(-2,3)= -0,1+2,3= -0,1+(-2,3)= 1,5-0,2= -1,5-0,2= 1,5-(-0,2)=...
1 - 1.Описать сюиту Пер Гюнт симфонию Героическую Л.В.Бетховнна (начало) и дать...
1 - 1.Построй экологическую пирамиду предложенного природного комплекса на выбор...
3 - Складіть формули оксидів за їхніми назвами : калій оксид , сульфур (Iv) оксид...
3
20
Пошаговое объяснение:
Известно, что сумма первых n нечетных натуральных чисел равна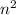 (это можно получить, например, из формулы для суммы арифметической прогрессии. Тогда
(это можно получить, например, из формулы для суммы арифметической прогрессии. Тогда
Приравниваем:
Вот альтернативный получить выражение для суммы из условия: это арифметическая прогрессия с разностью 2, в которой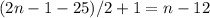 членов. Сумма равна полусумме крайних членов, умноженной на количество:
членов. Сумма равна полусумме крайних членов, умноженной на количество: