Найти корни уравнения 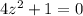 и разложить квадратный двучлен на множители.
и разложить квадратный двучлен на множители.
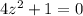
Другие вопросы по теме Математика
Популярные вопросы
- Как правильно пишут слова кукушка и подушка...
3 - Решите из 2 городов расстаяние между которыми 846 км выехали на встречу друг другу...
2 - Подобрать 2 пословицы на к тексту ыбрая алтынсарина әке мен содержание рассказа:...
2 - Какое слово(а) образовано приставочно-суффиксальным по-дружески,никогда,отчётливо,позавчера...
1 - Предложения со словами приятельский.манера.публика.безделица...
2 - Постройте ось симметрии: а) отрезка; б) угла; в) прямой....
1 - Выражение: 6a(a-x-c)+6x(a+x-c)-6c(a-x-c)...
2 - Не решая уравнений запиши их в порядке увелечения корней 219+(e+325)=935 219+(e+282)=935...
1 - Составить слова или слово из букв е о т ц е р р б ь о (одна буква лишняя) !...
3 - Кто из этих богов громовержцов, настоящий бог громовержец? перун, нептун, зевс,...
1
z1= i/2
z2=-i/2
Пошаговое объяснение:
4*z^2 +1 = 4*z^2 - (-1) = (2z)^2 -(i)^2 = (2z-i)*(2z+i)
(2z-i)*(2z+i)=0
z1= i/2
z2=-i/2
(см. объяснение)
Пошаговое объяснение:
Получили, что уравнение не имеет корней на множестве действительных чисел, поскольку число в квадрате есть число неотрицательное.
Разложить на множители можно так: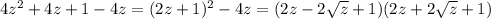
Если нужно решение с комплексными числами, то:
Тогда разложить на множители можно так: