Найти координаты вектора X в базисе e'1, e'2, e'3, если он задан в базисе (e1, e2, e3). 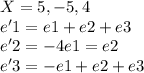
Другие вопросы по теме Математика
Популярные вопросы
- Хронологічна послідовність формування провідних політичних сил в українському...
1 - Нужно решить все задания ...
1 - решить,(учебник география просвещение 7класс, 2015 год)...
3 - ГЕОГРАФИЯ В чём заблуждался Х.Колумб?...
3 - Task 3. Write the letters in numbers. 1. Seven hundred seventy five...
3 - поставьте глаголы в Present Perfect Simple:bemake take seedoreadwinwatch...
1 - Хлопчик має 6 лампочок, які розраховані на напругу 6В. Джерело живлення...
1 - Укажи масу етану який згорить якщо витратилось 21,7 моль кисню...
3 - Перевод: 6. ( ) По названию составьте структурные формулы следующих...
2 - Ребят Что делать если нанюхался уксусом при чистке утюга, вся семья...
1
Матрицу перехода можно составить из координат векторов базиса (e'1, e'2, e'3) в базисе (e1, e2, e3). Для этого воспользуемся формулой:
[ [e'1] ] [ [e'2] ] [ [e'3] ]
| e1 | * | e2 | * | e3 |
Заменим в этой формуле векторы базиса e1, e2, e3 соответствующими координатами:
[ [e'1] ] [ [e'2] ] [ [e'3] ]
| 1 1 1 | * | -4 0 0 | * | -1 1 1 |
| 1 0 0 | | 0 1 0 | | 1 0 1 |
| 0 1 1 | | 0 0 1 | | 1 1 1 |
Выполним произведения и получим матрицу перехода:
[ [e'1] ] [ [e'2] ] [ [e'3] ]
| 1 1 1 | * | -4 0 0 | * | -1 1 1 |
| 1 0 0 | | 0 1 0 | | 1 0 1 |
| 0 1 1 | | 0 0 1 | | 1 1 1 |
= [ [e1] ] [ [e2] ] [ [e3] ]
| -4 0 0 | * | 1 1 1 | * | -1 1 1 |
| 0 1 0 | | 1 0 0 | | 1 0 1 |
| 0 0 1 | | 0 1 1 | | 1 1 1 |
= [ -4 4 4 ]
| 1 1 1 |
| 1 1 2 |
Теперь у нас есть матрица перехода от базиса (e1, e2, e3) к базису (e'1, e'2, e'3).
Чтобы найти координаты вектора X в базисе (e'1, e'2, e'3), нам нужно умножить матрицу перехода на вектор X:
[ -4 4 4 ] [ 5 ]
| 1 1 1 | * |-5 |
| 1 1 2 | | 4 |
= [ -4*5 + 4*(-5) + 4*4 ]
| 1*5 + 1*(-5) + 1*4 |
| 1*5 + 1*(-5) + 2*4 |
= [ -20 + (-20) + 16 ]
| 5 + (-5) + 4 |
| 5 + (-5) + 8 |
= [ -24 ]
| 4 |
| 8 |
Таким образом, координаты вектора X в базисе (e'1, e'2, e'3) равны (-24, 4, 8).