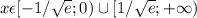Найти интервал возрастания и убывания функции: y=x^2×lnx
Другие вопросы по теме Математика
Популярные вопросы
- 40%территории нашей страны занимают пустыни .Будет ли пустыня расположенная...
1 - 5.Из приведённые ниже акынов выберете относящихся к эпохе «Зар заман»...
2 - Розв‘яжіть будь ласка ів тільки давайте без приколів...
2 - Решить и найти наименьшее решение неравенства У МЕНЯ СОЧ...
3 - не виконуючи побудови графіка функции у =5х-2 визначити через які...
3 - Мәтінді оқып, тапсырмаларды орындаңыз Қыз бала тәрбиесінде ананың...
1 - Країни-виробники та країни-експортери тканин, одягу, взуття...
1 - 6°. Чому дорівнює скалярний добуток векторів а(2;-3) та в(-3;-4)...
2 - көмектесіп жібере аласыздар ма ...
1 - Контрольна робота з української мови 7 клас прислівник...
1
Возьмём производную. Если производная в данной точке больше 0, функция растёт и наоборот.
Если подлогарифмическое выражение больше 1, то логарифм больше единицы.
Если логарифм больше 0, то при отрицательных х производная меньше 0 (x<-1/sqrt(e)), при положительных - больше 0 (x>1/sqrt(e)).
Если логарифм меньше 0 (|x|<1/sqrt(e)), то при положительных х производная меньше 0 (0<x<1/sqrt(e)), при отрицательных - больше 0 (-1/sqrt(e)<x<0)
В крайних точках функция определена (кроме х=0), значит интервалы включают крайние значения.
Функция убывает при![x\epsilon(-\infty;-1/\sqrt{e}]\cup(0;1/\sqrt{e}]](/tpl/images/0150/0553/0bd51.png)
Возрастает при