Найти интеграл $\int\limits{\frac{1}{x^{2}-\frac{1}{2} } } \, dx$ с подробным решением

Ответы

Sillyteenager 17.07.2020 06:59

Из таблицы интегралов: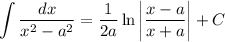 $\displaystyle \int\dfrac{dx}{x^2-a^2}=\dfrac{1}{2a}\ln\bigg|\dfrac{x-a}{x+a}\bigg|+C$

Применим эту формулу

$\displaystyle \int\dfrac{dx}{x^2-\left(\frac{1}{\sqrt{2}}\right)^2}=\dfrac{1}{2\cdot \frac{1}{\sqrt{2}}}\ln\bigg|\dfrac{x-\frac{1}{\sqrt{2}}}{x+\frac{1}{\sqrt{2}}}\bigg|+C=\dfrac{1}{\sqrt{2}}\ln \bigg|\dfrac{x\sqrt{2}-1}{x\sqrt{2}+1}\bigg|+C$

ПОКАЗАТЬ ОТВЕТЫ

DaryaKareva 17.07.2020 06:59

Это табличный интеграл ∫dx/(x²-a²)=(1/(2a))*㏑I(x-a)/(x+a)I+c

∫dx/(x²-(1/2))=∫dx/(x²-(√2/2)²)=(1/(2*(√2/2)))*㏑I(xx-√2)/(x+√2)I+c=

(√2/2)*㏑I(2x-√2)/(2x+√2)I+c=(√2/2)*㏑I(√2(x√2-1))/(√2(x√2+1)I+c=

(√2/2)*㏑I((x√2-1))/((x√2+1)I+c

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

sorokovilya 20.12.2019 09:19

Из 45 кг хлопкового семени получили 11,25 кг масла. определи, сколько масла получится из 9 кг хлопкового семени....

semaf1345789 20.12.2019 09:17

1. точки максимума функции у = ln(x2 + 1) 1) 02) +-13) точек максимума нет4) 0,+-1...

irunadp0a62f 20.12.2019 09:15

Скорость первого автомобиля 12 км/ч, скорость 2 автомобиля 15 км/ч. время движения 3 ч. найдите расстояние! ...

nodiramahammadz 20.12.2019 09:14

Вчетырехугольнике abcd сторона ab неизвестно то есть x выразите остальные стороны этого четырёхугольника если все на 3 см меньше a b c d на 2,5 раза больше ab мк на 2 см больше cd...

KristinaPanpi4 20.12.2019 09:13

Найдите среди чисел 1 3/5; 2 6/9; 8/9; 5/8/2 5/8...

vanyakolesov1 20.12.2019 09:12

Решите : пешеход весь путь за 2,5 часа со скоростью 3,6 км/ч. сколько времени он потратит на этот же путь если будет идти со скоростью 5 км/ч...

araitokbasova 20.12.2019 09:11

Туристы проехали 150 км. в первый день они проехали 2/3 всего пути. сколько км туристы проехали во второй день...

asik1602 20.12.2019 09:11

(49+21): 7 ар турли тасилдердин биримен есепте...

BOGDANGER 20.12.2019 09:09

6-га калдыксыз болинетн еки сандардын косындысын тап...

Акбота1ю 20.12.2019 09:08

При каком значении р прямые зх + 4у -7 =3d 0 и рх -зу-1 =0 перпендикулярны....

Найти интеграл с подробным решением

Популярные вопросы

Найти интеграл $\int\limits{\frac{1}{x^{2}-\frac{1}{2} } } \, dx$ с подробным решением