Найти градиент функции z=x/x^2+y^2 в точке м0 (1; 2)
Ответы
Градиент - это вектор из частных производных функции
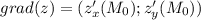
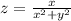
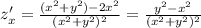
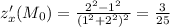
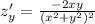
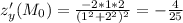
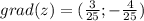
ПОКАЗАТЬ ОТВЕТЫ
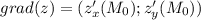
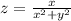
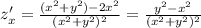
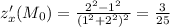
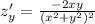
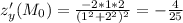
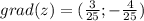
Другие вопросы по теме Математика
Популярные вопросы
- Что такое металлургический комплекс?...
3 - Выберите лишнее звено в цепочке и объясните свой ответ: а) афанасий...
1 - Вычислите - 42,71- 2 целых 4/,,71)- 1 целая 5/9...
3 - Было 500р. потратили 40•/• всей суммы и 50•/• остатка. сколько денег...
3 - Составьте предложения, используя в качестве подлежащего словосочетания:...
2 - Вот : complete the sentences. make them true. 1) during our english...
2 - Як правильно пишется то хто живе в америці називається (американечь...
1 - Вкакое время суток автор увидел собор...
1 - Вот : complete the sentences. make them true. 1) during our english...
1 - Выразиет обычной дробью 0.2 0.6 0.25 0.375...
3