Найти эксцентриситет кривой, точки которой на комплексной плоскости определяются соотношением
l l z-2*i l - l z+2*i l l = 3
где z-комплексное число, l - модуль
Другие вопросы по теме Математика
Популярные вопросы
- Составить текст со словами : однажды,сначала,вдруг,затем,вскоре,опять,неожиданно,наконец....
3 - Волк,волчонок,волчий,волчок. найти корень и окончание....
2 - Нарисуй все чтобы разменять 10р. одинаковыми монетами достоинством по 2р...
3 - Сократите дроби: 75/100; 80/1000; 30/1000; 55/100; 55/1000; 30/100. нужно...
1 - Complete the sentences. put prepositions if necessary 1. my father is )...
2 - Нужно написать мини сочинение на про одну достопремичательность моей страны,...
1 - Удвух равнобедренных треугольников равны углы при вершинах. основание одного...
1 - Какую пословицу можно сложить из слов? записать вставляя буквы. в каких...
1 - Дробь 15/8 представить в виде десятичной дроби...
1 - Решить на проценты,с подробным ! p.s.с подробным ! 1. смешали 160 г раствора,...
1
Пусть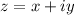 , тогда
, тогда
Возводим обе части уравнения в квадрат, получим
Снова возводя в квадрат и выполняя преобразования, мы получим
Это уравнение гиперболы, только действительная и мнимая полуоси лежат на оси ординат, т.е. сместили гиперболу вида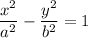 поворотом под углом 90°.
поворотом под углом 90°.
Тогда эксцентриситет: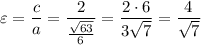
ответ: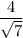 .
.