1. Математика
  2. Найти длину отрезка прямой

Найти длину отрезка прямой заключённой внутри эллипса​

terehovakira terehovakira    2   28.10.2019 02:20    27

Ответы
mery77 mery77  27.08.2020 15:55

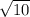
ответ: \sqrt{10}

Пошаговое объяснение:

Решим систему из тих двух уравнений для нахождения точек пересечения прямой и эллипса:

\left \{ {x+3y-21=0} \atop {\frac{x^2}{225}+\frac{y^2}{25}=1}} \right. \left \{ {x=-3y+21} \atop {\frac{x^2}{225}+\frac{y^2}{25}=1}} \right. \\\frac{(-3y+21)^2}{225}+\frac{y^2}{25}=1\\\frac{(-3y+21)^2+9y^2}{225}=1\\9y^2-126y+441+9y^2=225\\18y^2-126y+216=0 \ |18\\y^2-7x+12=0\\y_{1}=4 \ , \ y_{2}=3

Соответствующие x:

x_{1}=9 \ , \ x_{2}=12

Вычислим расстояние между двумя точками:

d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(12-9)^2+(3-4)^2}=\sqrt{10}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Kybe009 Kybe009  28.04.2020 12:26
1. Запиши числа в порядкеe убывания: 8470, 47800, 7408, 7840, 4807 . 2. Вычисли: 1700 : 25 + 502 х 130 3. Реши задачу: Печь выпекает 450 батонов за 30 мин. Сколько батонов...
goshan14 goshan14  28.04.2020 12:28
Відстань між двома селами становить 20 км. Артем пройшов пішки 1/4 шляху, а решту - проїхав на велосипеді. Скільки кілометрів хлопчик проїхав на велосипед? Как розвязати...
дарья2411по дарья2411по  28.04.2020 11:53
Какое число является корнем уравнения 2,7⋅x:0,003=4320?...
Caxapok24 Caxapok24  28.04.2020 11:53
очень нужно,прям вот в край...
YarikCage YarikCage  28.04.2020 11:53
Выразив переменную y через переменную x , найдите два каких-либо решение уравнения x+y-3=0; x+4y+12=0...
PrOFy100 PrOFy100  28.04.2020 11:53
Выберите из точек А, В, С и D точку с наименьшей абсциссой и точку с наибольшей ординатой. Запишите их координаты....
Рокистка068 Рокистка068  28.04.2020 11:54
Що є геометричним місцем точокрівно віддалених від точки А. прямащо проходить через точку А, відрізок із серединою в точці А, промінь із початком уточці А, коло з центром...
kotodrotin kotodrotin  28.04.2020 11:54
решить задачу с выражения​...
dfefert4tNNN dfefert4tNNN  28.04.2020 11:54
В течение дня почтальон разнесла 60 газет, журналов - в 5 раз меньше, чем газет и журналов вместе. А листов - у 4 рази меньше. Сколько писем разнесла почтальон в течение...
nikitakucherenk nikitakucherenk  28.04.2020 11:54
Определите координаты точек...

Популярные вопросы