Найти дифференциал функции:
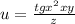
Другие вопросы по теме Математика
Популярные вопросы
- Записи названия разных веществ какие являются так рдыми жидкими газообразным...
3 - Много сказок и легенд народов посвящено янтарю. где тут сущиствительные?...
2 - Предложение со словосочетанием российское правитьльство...
2 - На решение двух васе потребовалось 24мин,а на решение трёх примеров на...
3 - Расчитайте какой объем оксида азота (lv) образуется при взаимодействии...
1 - Лесков говорил ,где стоит левша ,надо читать народ .имея это ввиду,подумайте,почему...
3 - Исправьте все ошибки рейтенг после арбитража,решоного не в пользу исполнитиля,понежаеться...
2 - За домом весело играл кот с маленькими котятами. 1. обозначь главные члены...
2 - 19стр 6 . каждый ученик нашей школы посещает один кружок. половина учеников...
2 - Выражение a в 7 степени делить на а в 3 степени...
2
Пошаговое объяснение: