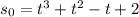Найти частное решение дифференциального уравнения:s´´= 6t + 2, если s = 3 и s´= 4 при t = 1
Другие вопросы по теме Математика
Популярные вопросы
- По вернуська до глежу во сне про хрустальный пишиться раздельно...
3 - Фрагмент днк состоит из 72 нуклеотидов определить число триплетов...
1 - Подобрать и поверочное слово к слову обнаженные...
3 - Как решить уравнения (х-83)+316=425, (600-х)-92=126, 253-(х-459)=138,...
3 - Ослик, пройдя по мосту 3/8 его длины, оглянувшись, увидел движущийся...
1 - Составить текст рассуждение на тему какой лес мне нравится и по чему...
3 - Рослыны яки показують погоду.реферат...
3 - Найдите стихотворение со словом штукатурка....
1 - За пытань вызнач звязок миж словамы беризка схылыла свои золоти виты...
1 - Почему незадолго до закипания чайника можно слышать характерный шум?...
1
Из начальных условий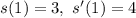 имеем:
имеем:
Частное решение:
ответ: