Найти частное решение дифференциального уравнения p(x) = 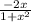
Q(x) = 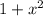
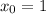
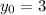

Другие вопросы по теме Математика
Популярные вопросы
- Complete using the correct form of verb in brackets. 1) Where (you/go)...
2 - Какие из перечисленных событий относится к попыткам создания системы...
2 - Составьте уравнение параболы с вершиной  М(2;-7) и фокусом Ф(3;5)...
1 - Определить виды предпринимательской деятельности 1. Решили организовать...
1 - с примером 25 × 25 ÷ 5 = ......
2 - 7.Найдите площадь прямоугольного треугольника, если его катет и гипотенуза...
2 - Найдите одночлен, равный сумме подобных одночленов: - 14,7а в квадрате...
3 - Визначити відносну молекулярну маму за формулами HS2...
3 - База данных содержит следующие записи: Какие из записей поменяются местами...
1 - Que ideoma ablan en kichwa...
3
общее решение
частное решение