Найти частное и общен решение дифференцированных уравнений уравнения (x^2+1)dy=xydx если y=2 при x=√3как решить уже целый час мучаюсь

Ответы

marialkahelp 09.10.2020 12:38

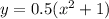
ответ: y=0.5(x^2+1)

Пошаговое объяснение:

Данное диф. уравнение является уравнением с разделяющимися переменными.... Разделим же переменные и затем проинтегрируем обе части уравнения

$\displaystyle \int\dfrac{dy}{y}=\int\dfrac{xdx}{x^2+1};~\Rightarrow~~\int \dfrac{dy}{y}=\int \dfrac{d(x^2+1)}{x^2+1}\\ \\ \ln|y|=\ln(x^2+1)+\ln C\\ \ln|y|=\ln(C(x^2+1)) \\y=C(x^2+1)$

Найдем теперь частное решение, подставляя начальные условия

$2=C((\sqrt{3})^2+1)\\ 2=4C\\ C=0.5$

y=0.5(x^2+1) — частное решение.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

ппсомо3657 06.04.2021 15:52

Высота прямого параллелепипеда равна 8 см, стороны основа- ния 3 см и 6 см и одна из диагоналей основания 5 см. С чертежа основания найди высоту основания и вычисли объемпрямого...

vladir03Wlad 06.04.2021 15:52

Розвязати рівняня |x|=6|x|=-2|x|=0|-x|=6,7 ів...

safiya250707 06.04.2021 15:52

Дрова нужно плотно уложить в штабель.Сколько чистой древесины содержится в штабеле‚размеры которого 3 м‚2м и 1 м? Сколько воздуха Было бы в штабеле‚если уходить дрова неплотно?...

elena444454 06.04.2021 15:52

1) Решите систему уравнений -x + 2y = 10 3y + x = 25 В ответе укажите меньшее из чисел х и у. 2) Решите систему уравнений -x - у = 9 Зх - у = 13 В ответе укажите меньшее из чисел...

вованоджи 06.04.2021 15:53

Площа малого поршня гідравлічної машини 8 см2, на нього діє сила 2 кН. Яку силу необхідно прикласти до великого поршня, щоб поршні були в рівновазі? Площа великого поршня 500 см2....

Amin1402 06.04.2021 15:53

До парка, который находится в центре города, можно доехать на самокате. Он проезжает 13,1 метр(-ов, -а) за одну секунду. Сколько километров этот самокат проедет за час? (ответ...

XxXRePlayXxX 06.04.2021 15:53

5×-6+ × =(× - 1) 50 - 7y - 16 = 3y - 16...

Hilet 06.04.2021 15:53

номер 1241. 1)Запишите число 15 в виде суммы двух положительных слагаемых сколько вариантов суммы можно записать...

ghui1 06.04.2021 15:53

Найдите координаты точки пересечения прямой, заданной уравнением: y = − 5/6x-7 с осью Oy...

ArseniyRich 06.04.2021 15:53

308:(а+в)*308:(а-в) (с+в):8*( с+в)×8 408:4+в*408:(4+в)...

Найти частное и общен решение дифференцированных уравнений уравнения (x^2+1)dy=xydx если y=2 при x=√3как решить уже целый час мучаюсь

Популярные вопросы