Найдите значение параметра a, при которых уравнение 3*x + 4 * sqrt(1-x^2) = a имеет хотя бы один корень

[-5; 5]

Пошаговое объяснение:

ОДЗ:

Пусть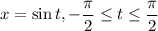 . Так как область значений синуса совпадает с областью значений (ОДЗ) x, потери корней не произойдёт. В силу ограничений на t на данном промежутке синус — монотонная функция.

При указанных значениях t косинус неотрицателен, поэтому модуль раскрывается с плюсом:

Пусть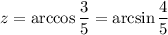 . Тогда

Уравнение имеет хотя бы один корень, если правая часть лежит в промежутке от -1 до 1: